temp

TAPESTRY: The Art of Representation and Abstraction

About Tapestry

The TAPESTRY pages are designed to provide a "variable depth" view of 3D computer graphics topics and technologies. As you browse the major topics listed along the left side of the screen, you will find additional detail opening up to you. While not replicating the detailed programming information provided in numerous excellent books on the subject, this work is intended to make available a knowledge-base about how the different modeling and rendering effects are achieved, and how these tools can be used to achieve design-presentation goals.

A simplified graphics application

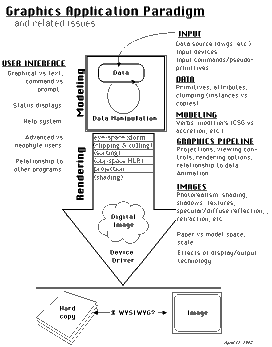This site is not designed to teach you the use of one particular program or system, though many of the projects are based in form•Z or StrataVision. It is to teach you how to learn about graphics programs in general, since there is no way to predict what you will find yourself using in the months and years ahead.

One way to gain a general knowledge about graphics applications would be through in-depth learning about a series of programs (one is never adequate), but none of you have the time for that. We will learn, in some depth, a couple of programs. At the same time, and perhaps more importantly, I seek to help each of you build your "vocabulary" of computer graphics concepts and terms, and to accelerate the development in each of you of a generic mental model, or paradigm, of a graphics application.

This generalized application reveals the parts of a graphics application in a fashion which is similar to the study of biological systems in an animal: i.e., circulation, digestion, nervous system, skeletal system, etc. We know they exist, and they help us understand the whole, but they don't represent the effect of the whole.

Input:
Intimately tied to the data, the process of data input is one of identifying the primitives of which the model is made, indicating their positions, sizes, colors, etc, whether the primitive is a "key frame" or a "polygon". Closely tied to the input process are questions of "input modification" (grid, object, and associative snaps, ortho and closure modes, etc.) which help the program decipher what we "mean", as opposed to what we "say", and vastly improve the precision of what can be said in a very small surface (the screen). Data: We will examine data ranging from simple vector entities in 2D ("lines, circles, arcs and text") to simple 3D polylines and polygons. We will look at the difference between true (data) primitives and "pseudo primitives" created in the user interface as a quick way of entering data, and we will look at "super primitives" defined by the user.

We will look at the concepts such as layers and their usefulness in structuring data for different kinds of access. We will also discuss the role of orientation or handedness in polygon data and we looked a little at how "positive data" fails to cover all the kinds of information we might be interested in.

We may have time to look at other 3D geometries, like "surface patches", NURBS, etc., which are more appropriate to disciplines dealing in complex surfaces (like cars and planes), and we will look at solid modelling, in which you really can have "negative data".

Modeling:
Crucial to the success of efficient computer application, beyond being able to clump data as we wish, is being able to rapidly generate additional data from existing data through modeling commands. We will look at simple examples of modeling commands (extrusion and revolution) as well as some less simple ones.

Rendering:
A numeric description of geometry within a computer program may be useful for some purposes, but visualization is one of the main reasons we create geometric models. We will come to understand that this process is controlled by a "view vector" which defines the location of the eye (camera) and focal point. There are many ways to define and adjust this information, but all projective systems require it.

The points which define the geometry are then "projected" from 3D to 2D, providing points in the image plane to form the outlines of polygon or the end-points of lines. "Backsiding" hidden-surface removal techniques help dispose of unwanted lines by discarding polygons facing "away" from the eye. Other hidden-line techniques operate in different ways. Some of these work in "data space" (using nearly infinite resolution), while others operate in "image space" (using finite, usually screen, resolution). Choice of technique effects hardcopy results and correctness of the rendering.

Rendering in image space introduces techniques which calculate individual pixel colors or intensities. This makes casting of shadows easier, as well as the apparent smoothing of faceted geometry. At the high end, raytracing reverses the trajectory of light backwards through the scene, discovering the contribution of light at each pixel. Each rendering algorithm has strengths and weaknesses. One works best in highly shiny, reflective environments, where another might work best in diffuse-reflection settings. Some permit use of other raster images as "wall paper" on the geometry, where others do not.  

 

Last updated: April, 2014

Valid HTML 4.01 Transitional Valid CSS! [report bug]