BMAD means "Bone Mineral Apparent Density" which is important when measuring bone density in children or in patients with short stature. Another term for this concept is "volumetric bone density".
Jones, 2006 found that spine BMAD had the strongest and most consistent association with upper limb fracture risk in children. Crabtree, 2013 found that BMAD was best predictor of vertebral fractures in children, and the total body less head, adjusted for height, was best for long bone fractures
L1-4 BMD --- T-score ---
L1-4 BMAD ---
T-score (USA database) ---
T-score (UK database) ---
The following calculations used the "block method" described by Bachrach, with a smaller database.
This was the method used in the previous BMAD calculator
BMAD for spine L2-4 --- T-score ---
Fem neck BMAD --- T-score ---
Kindler, 2019 reports reference ranges for BMAD in 2014 children from the United States, using Hologic machines. They used the method of dividing the sum of the mineral contents by the sum of the calculated volumes of the 4 lumbar vertebrae.
(L1BMC + L2 BMC + L3 BMC + L4 BMC) / (L1V+L2V+L3V+L4V)
For each vertebra the volume is the area raised to the 1.5 power.
The values were not normally distributed, so to account for skewed data, they reported LMS parameters to calculate the Z-scores, using this complicated equation
Z = [(y/M)L -1] / L*S
The value that would be a standard deviation in a normal distribution would be approximately half the distance between the median and the 98th percentile. (If you read this reference paper, be aware that they mistakenly said that the "S" parameter is the "SD", but it is actually the generalized coefficient of variation, not the standard deviation.)
In 20 year old non-Black females the median BMAD was 0.269 g/cm3; the L was -0.057 and S was 0.096. The approximate standard deviation from the graph was 0.028. The median BMD was 1.024 g/cm2 with approximate SD of 0.09 (Zemel, 2011). Remember that by convention, in the bone density field, the T-score is the same as the Z-score of white females at peak bone mass (around 20 to 25 years of age.
This compares to the NHANES normative data for the spine of 1.047 ± 0.11 g/cm2 (Looker, 2012).
Crabtree, 2016 report BMAD from 3598 children in the UK, using both Lunar and Hologic machines. They found that the equations to convert the Lunar to Hologic results were not very accurate, so there are different normal ranges for each type of densitometer. They used the same equations as above.
For nonBlack females aged 20 on a GE Lunar Prodigy the median BMAD was 0.329 g/cm3, L was -0.01 and S was 0.10. The standard deviation would be approximately 0.030. On a Hologic the median BMAD was 0.261 g/cm3, L was 1.00 and S was 0.11. The standard deviation is approximately 0.025.
The corresponding median BMD values were 1.189 g/cm2 for Lunar and 1.008 g/cm2 on the Hologic.
In Black children of all these studies the bone density and BMAD are higher; at age 20 the average Black young woman is one standard deviation higher than the average for non-Blacks.
We had estimated the "volumetric bone density" based on dimensions on xrays and calculated volume as: height x width x depth x pi/4. (Ott, 1988)
The term BMAD was defined by Carter, 1992 using this equation:
(L2BMC + L3BMC + L4BMC) / ((L1Area+L2Area+L3Area)1.5)
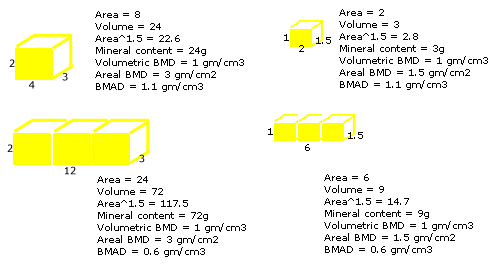
I call this the "block method" as shown in the diagram below, which gives lower results than the "individual vertebra" method. Using this definition, Bachrach, 1999 reported the BMAD in 423 normal children. In white females age 23-26, the mean BMAD was 0.164 with standard deviation (SD) 0.022. They also calculated a BMAD for the femoral neck as BMC/Area 1.5. The mean was 0.174 ± 0.028. These were the references that I used to calculate a BMAD T-score for the previous calculator. The equation for the T-score is simply:
(BMAD patient - BMAD reference mean)/standard deviation reference.
Note that the spine BMD was 1.074 ± 0.117 gm/cm2.
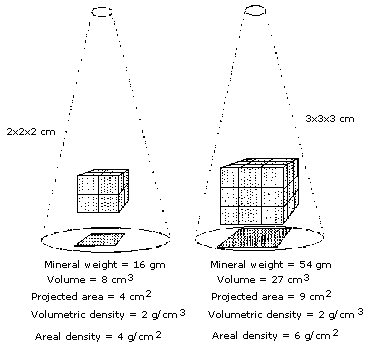
The DEXA technique analyzes the attenuation of xrays as they pass through an area of the body. The method cannot detect the depth of the bone which is being measured, and thus is actually an "areal" density in g/cm2 rather than a "volumetric" or Archimedean density in g/cm3. As bones grow, the volume increases at a faster rate than the area, so the areal bone density will increase even if the volumetric density remains stable.


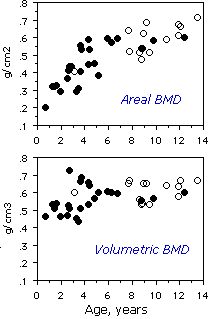
The graph is from our study of young primate vertebra, in which volumetric density did not show much change with age, although the areal bone density suggested an increase with age.
Vertebrae are not simple cubes, but complex shapes. In our study, we measured both the vertebral dimensions and the volume of the entire vertebra, and found that the volume was predicted quite well by simply multiplying the height x width x depth of the vertebral body. However, when measuring bone with DEXA, the depth is not known. The depth of a single vertebra can be estimated as the square root of the area, which is the basis for calculating volumetric BMD. The formula is:
BMC/area^1.5 (where area^1.5 is the area times the square root of the area).
In our studies we calculate the volumetric BMD for each lumbar vertebra and take the average. At Stanford, they took the results for 3 vertebrae (L2-4) as a block, and called this the BMAD. The BMAD is therefore lower than the volumetric BMD by a factor of 1.73 (the square root of 3).
Another problem with estimating the volume from the area is that the shape of the vertebra changes with growth - in other words, the growth rate of the height of the vertebrae is different from the width of the vertebrae. The best volumetric bone density is measured using QCT, but that technique has other problems with radiation and reproducibility.
BMAD probably does not predict fractures in postmenopausal women any better than areal BMD, so it is not necessary to use BMAD clinically for ordinary-sized adults. But in adults shorter than 5 feet, the areal BMD can be very misleading. For example, we studied patients who were very short due to mutations in the growth hormone receptor, and found that the BMAD was similar to unaffected family members, whereas the areal BMD was much lower. The bone volume/tissue volume from bone biopsies in these patients was normal, providing validity to the BMAD results (Bachrach, 1998).
Updated 3/17/21
