Big O Lab 9
CSS 162: Programming Methodology
Autumn 2012
Instructor Rob Nash
Summary
In this lab, we will evaluate code with respect to the Big O techniques we’ve covered in class. We’ll examine code to determine the total number of operations the code takes with respect to input size n. This will produce a function f(x) (a polynomial) whose worst-case is unknown. It will be up to the reader to select a second function (g(x)) from a list of reference functions and show that, for some integers c and k,
| f(x) | < c | g(x) | when x >k
If we can demonstrate this above, then we have proven that our unknown function f(x) is a member of the set O( g(x) ), where g(x) is our known reference function.
Reference Functions for g(x)
{ 1 , log n, n, n log n, n2, n3, …, n!, nn }
Big O Operations (Arithmetic, Relational, Logical)
{ + , - , ++, -- ,* , / }
{== , != , < , > , <=, >= }
{ & , && , | , || , ! }
{ =,[] }
Introduction
We are interested recognizing a set of operations that can generalize well to multiple different hardware platforms. These operations invoke the ALU inside of the CPU and represent a basic computational “step” in a traditional load-store architecture (ie, a von-neuman architecture). Let’s put this into practice and count the number of operations that occur in a basic for loop.
for(int a = 0; a < 10; a++) { //how many operations occur each loop iteration?
d = a + a; //how many operations occur on this line of code?
}
Big O Reduction Rules
· Addition Rule: If a segment of code a(x) is represented by the sum of two disjoint code sections f(x) and g(x), then the O(a(x)) is equal to the larger of the two : O(f(x)) or O(g(x))
o Specifically, O(a(x)) = Max(O(f(x), O(g(x))
·
Product
Rule: If a segment of code a(x) is represented by
the product of two (nested) code sections f(x) and g(x), then the O(a(x)) is
equal to the product of the two : O(f(x) * g(x) )
o
Specifically, O(a(x)) =
O(f(x) * g(x))
·
Log
Exponent Rule: Consider the
following logarithm a(x) = log2Xc. Note that we can rewrite this using the “log
roll” as c*log2X. Since
constants are factored out during asymptotic analysis, you can simply drop the
constant multiplier (which on a log is it’s exponent).
·
Log Base
Rule: You may omit the base of the
log and assume its base-2.
·
Transitivity:
if a < b < c, then a < c.
Related to big O, if a = 5x2+3x and I’m trying to prove that
a is less than or equal to (ie, bounded by) x2,
we would write 5x2+3x < c * x2 and find some pair
of c,k such that this relationship holds. Using transitivity,
o
5x2+3x < c * x2
o
5x2+3x < 5x2+3x2
< c*x2
o
5x2+3x < 8x2 <
c*x2
§
Now simply choose c (==8) and k(==1)
Estimating g(x) Given f(x)
In the following section, indicate what reference function (g(x)) we should use when attempting to prove that f(x) is O( g(x) ). Use the rules and reference functions above to guide you.
(1) f(x) = n + Log2n
(2) f(x) = n2 + Log n4
(3) f(x) = n2*n3
(4) f(x) = n5/n2
(5) f(x) = n*(log n) *n
(6) f(x) = n + n log n + log n
Counting Operations to Produce Polynomials
In the following section, I will present you with multiple different bodies of code, and it is your job to analyze each code section and build a polynomial that represents the number of abstract operations the code performs. Once we’re done here, we’ll have build a polynomial that we will analyze further (in terms of g(x), c, and k) in the next section. For the following code segments below, count the operations and produce a corresponding polynomial representation.
f(x) =
f(x) =
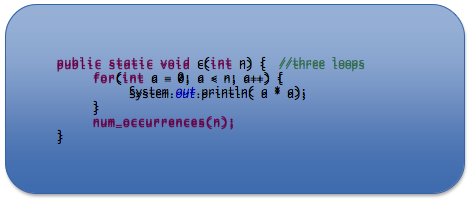
f(x) =
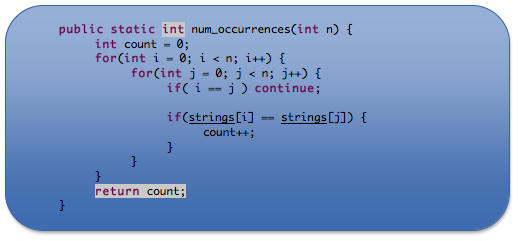
f(x) =
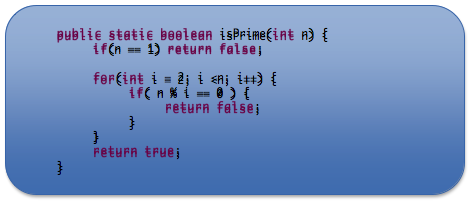
Demonstrating | f(x) | < c | g(x) | for all n > k
For each of the polynomials above, pick a reference function (g(x)) and constants c,k such that the g(x) bounds f(x) in the most succinct terms possible for Big O.
(1) For the function a() above, what is…
g(x) =
c =
k =
(2) For the function num_occurrences() above, what is…
g(x) =
c =
k =
(3) For the function c() above, what is…
g(x) =
c =
k =
(4) For the function isPrime() above, what is…
g(x) =
c =
k =
Exam Practice
(5) For your Bubble Sort, what is…
f(x) =
g(x) =
c =
k =
(6) For your Selection Sort, what is…
f(x) =
g(x) =
c =
k =
![Rounded Rectangle: public static int num_occurrences(int n) {
int count = 0;
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if( i == j ) continue;
if(strings[i] == strings[j]) {
count++;
}
}
}
return count;
}](lab9_files/image001.png)