Lab 6
CSS 162 : Programming Methodology
Winter 2013, Instructor Rob Nash
Recursion, Part I
Summary
The purpose of this lab is to practice transforming recurrence relationships into working Java code. Start by reviewing the example code to gain an intuition and understanding for recursive behavior, and then build your own custom recursive methods.
Summation: An Example Recursive Function
Download the following classes for this lab: {RecursionLab.java}. In the main function, experiment with the two variations of summation functions (iterative versus recursive) by commenting and uncommenting the desired code paths. Read the comments throughout the code before moving on to modify this algorithm, and consider how you might rewrite the recursive function as an iterative function and vice versa.
From Summation to Factorial
The definition of the factorial function is defined below. Using the summation code as a guide, write a very similar recursive method that calculates the factorial of some input n. This method should be like all recursive functions in that it (1) knows how to solve a trivial (base) case, and (2) it knows how to decompose larger cases into smaller cases. Frequently, this translates into an “if” statement that has the form:
if(1) {
return base case solution;
} else (2) {
result = recursive call
return result;
}
Build this new recursive method and test your code with a short main driver.
The Exponent Function
In this section, we will build two recursive functions and roughly compare their respective performance. Write a method that produces the result of xn by observing the following recurrence relationships:
(1) x0 = 1
(2) xn = x * x(n-1) when n > 0
Verify your method produces the correct value by writing a main that tests it. In the same class, write another function that will also recursively solve for exponential values, but will do so by cutting our problem in half at each step (rather than moving the solution along incrementally by subtracting one from n at each step). This new relationship is defined by the piecewise function:
(1) x0 = 1
(2) xn = ( x(n/2) )2 when n is even
(3) xn = x * ( x(( n-1 )/2 ) )2 when n is odd
To obtain the desired speedup, make sure your new function recursively calls itself no more than once in the body of the method. Once you have built this new recursive method, you should be able to redirect your main to test its output. Do so, and compare the execution times for large n with the old implementation – which is faster, and why?
Combinations, or “N Choose R”
Given a set of n items, how many ways can we pick r elements from n? This is known as the “choose function” (or binomial coefficient), and we can calculate the number of r-sized subsets of n (where order is unimportant) using the recurrence relationship defined below. Note that this definition builds on the notion of factorial, so make sure you understand the sample code first and have produced a working factorial method before moving on.
C(n,r) = n! / ( r! * (n-r)! )
You can create a faster solution to this problem if you reuse the individual component calculations (rather than re-calculating these), which are r! (less than n!) and (n-r)! (also less than n!), but this is merely an observation and not to be implemented as part of the lab.
The Fibonacci Numbers
This series is described with by the following recursive relationship:
f(0) = f(1) = 1
f(n) = f(n-1) + f(n-2) for n > 1
The above formulae produce the following output “1 1 2 3 5 8…” for some n (>4), and can be systematically calculated using a recursive function. Write a function Fib(n) that prints out the corresponding sequence of Fibonacci numbers , and write a main that invokes this function with some sample values of n.
Fractals & Depth-Limited Recursion
In this next section, we’ll create a new Shape Subclass that uses recursion to create a fractal snowflake pattern. We’ll manage the size of our flakes (as well as the number of recursive calls) using an integer called “size”. This value will provide us with a way to abort the recursion after a specified number of recursive calls – this technique is known as depth-limited recursion, and is frequently used in graphics applications such as fractal design and reverse ray-tracing.
1. Download PolyDemo.java and Shape.java from the last homework.
2. Build a new class called FractalFlake.java that extends Shape
a. Define a private final int to manage the snowflake’s size.
i. These should be values such as {1…50}
b. Define a second private final int to manage the number of branches for the flake
i. These should be between {5..12}
3. Build a suitable constructor for FractalFlake that invokes the superclass constructor as the first line of code.
a. In our examples, these flakes will have a size variable, which you should pass to the constructor for your FractalFlake to store
b. Our FractalFlake also has a branching factor, which should be handed to the constructor for our class to manage.
4. Override the draw function so that it invokes a second draw function that takes more parameters than just the Graphics object, as in:
@Override
public void
draw(Graphics g) { //a redirect or
facade
draw(g,getX(), getY(),size);
}
5. Overload the draw() function by defining a new draw function that takes a starting x,y coordinate pair, a size, and a graphics object to render to, as in:
private void
draw(Graphics g, int startX, int startY, int size) {
if(size >= 3) { //base case is depth <3
for ( int i = 0; i
< numBranches; i++ )
{
int x2 = startX
+ (int) (size *
Math.cos( (2 * Math.PI / numBranches) * i ));
int y2 = startY
- (int) (size *
Math.sin( (2 * Math.PI / numBranches) * i ));
g.drawLine( startX, startY, x2, y2 );
//do a branch
draw(g, x2, y2, size/3);
//recursive call
}
}
}
6. Finally, modify the PolyDemo driver so that in the getRandomShape() function, you can produce FractalFlakes as well as Sprays.
7. This type of recursion is limited by the value “size” – when we’ve divided size enough times, eventually we will arrive at our base case (size<3). In this way the size variable provides a limit on the number of times the function will call itself; hence the name “depth-limited recursion”
8. Execute your driver and verify your recursive fractal patterns visually; this should look something like the snowflake patterns below.
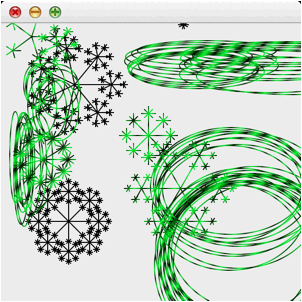
File Searching
In general, searching can take multiple forms depending on the structure and order of the set to search. If we can make promises about the data (this data is sorted, or deltas vary by no more than 10, etc.), then we can leverage those constraints to perform a more efficient search. Files in a file system are exposed to clients of the operating system and can be organized by filename, file creation date, size, and a number of other properties. We’ll just be interested in the file names here, and we want perform a brute force (read: linear) search of these files looking for a specific file. The way in which we’ll get file information from the operating system, there will be no imposed ordering; as a result, a linear search is the best we can do. We’d like to search for a target file given a specified path and return the location of the file, if found. Lets sketch out this logic linearly before we attempt to tackle it recursively.
Pseudocode
Push the given directory on the directory stack
while(stack is not empty) {
Pop off a file or directory.
If a file, check for a match and return if found
If a directory,
for(Every file and directory in the directory) {
if a directory, push on the directory stack
If a file, check for a match and return if found
}
} //end while
return not found
File Search, Version 1.0
Build a linear search following the pseudocode approach above. You can put this code in simply a main, or you could design a static helper function in your HP static class that searches for files. Did you notice we used a stack to accomplish this directory searching? Using the main below and the outline above, complete the iterative file searching algorithm in the method searchFiles(). Use fileObject.listFiles(), fileObject.isDirectory(), and fileObject.getName() to accomplish this below.
public static void main(String[] args) {
System.out.println( searchFiles(new File(“c:\\”), “hw3.zip”) );
}
public static String searchFiles(File path, String target) {
//todo
}
File Search, Version 2.0
We made use of an explicit stack to track new directories as they appear in the above iterative code. Do you think we could use the method call stack in place of our Java stack to accomplish this recursively? If we remove the stack definition and code above and produce a recursive function, might that be shorter? Change the main function above to call recursiveSearch() instead, which is a new method that you will create. This method will take the same input as searchFiles, but instead of searching through files using explicit for loops and a Stack from java.util, we’ll be using recursive function calls to facilitate some of the looping and use the method call stack to store our directory list instead. Build a recursive linear search following the pseudocode approach below.
public static String searchFiles(File path, String target) {
check if path is actually a dir, abort if not
loop over all files in the directory
if a file, check for a match and return if found
if a directory, call this function again with the new directory
if the directory search above produced a match, return
return “Not found”; //if we made it here, we didn’t find it
}
The Linear and Binary Search Homework Head Start
Both searches that you will implement for your next homework can be done either iteratively or recursively. Read the next assignment now, and design an iterative version of the linear search. Once you have this working, convert your iterative algorithm to a recursive one. Once this is complete, try to design an iterative binary search using the code provided for you for the Binary Search HW.
(1) Build an iterative linear search
(2) Convert your iterative search to a recursive linear search
(3) Build an iterative binary search (use my interface as defined in the HW)