CSS 343: Notes from Lecture 4 (DRAFT)

Our story so far: finding stuff by value is such a useful operation that we give it various names, including dictionaries, symbol table, lookup table, associative array, map, set, relational database, and hash. We can implement a dictionary abstraction using a linked list, but this give O(N) asymptotic performance for lookup—relatively expensive unless N is pretty small or we're doing a small number of lookups. We can use binary search in an array but this is inflexible. We can exploit the basic idea of binary search to build a data structure called a Binary Search Tree (BST).

As with Binary search, search tree algorithms require that the stored data has an ordering predicate which we can call "less-than" without loss of generality.

A BST works well (O(log N) lookup) as long as the input while building the tree arrives in random order (average case). The tree can degenerate into a linked list for large classes of systematic input, including common cases such as input in sorted or reverse sorted order.

We have several algorithms that rebalance the tree via rotation operations.

The B Tree uses a different approach for balancing. We will look at the 2-3 tree as a special case.

AVL Tree

The AVL tree is the original self-balancing data structure, discovered/invented in 1962 by G. M. Adelson-Velski and E. M. Landis. Insert/Lookup/Delete are O(log N) for best, worst, and average cases.

We won't go into detail about the AVL, because we'll focus on the red-black tree. We just note the basic idea and the essential difference between AVL and red-black.

The basic idea is that each node keeps track of difference in height between the two subtrees. On insert or delete, rotations are performed to maintain a difference of no more that 1, keeping the tree roughly balanced. The lookup operation is unmodified.

Since the tree is balanced, insert/delete is O(log N). To rebalance after an insert, we perform up to O(log N) rotations, so the net asymptotic complexity remains O(log N).

• same asymptotic complexity but AVL trees are more rigidly balanced than red-black Trees:
  • insert/delete is more expensive than RB
  • lookup is cheaper than RB
• performance differs by a constant factor, which falls out when looking at big-oh performance, but may still be important when assessing actual performance

Red-Black Trees

Also see the wikipedia article.

A red-black tree is a Binary Search Tree in which each node is labeled by a color, red or black (it could be called up/down, true/false, 0/1, but red/black was chosen). The tree has the following rules (invariants) that must be maintained:

• the root is black
• synthetic black leaves are added to fill in every null child of the original tree.
  • a single shared object may be used to save memory
• all simple paths from a node to it's leaf descendants have the same number of black nodes (black height)
• the children of any red node must be black

Implication:

• The longest path will be no more than double the length of the shortest path giving O(log N) insert/lookup/delete, provided we can rebalance in O(log N) time after insert/delete.

A parent pointer is not required, but makes coding so very much easier.

Trying to hand-label some arbitrary binary tree is hard and confusing

• not every binary tree can be labeled as a red-black tree
• rotations may be applied to Binary tree to transform it into a red-black tree

Insertion

Considering only insertion; deletion is similar.

Insert a new entry in the tree in the location where it would normally be inserted (ignoring the synthetic black leaves). Label the new node red. It will have two black (synthetic) children. Rebalance the tree to make sure the red-black conditions (invariants) are maintained.

• insertion may require O(log N) color changes.
• insertion may require O(1) tree rotations (2 rotations for insert, 3 for delete)

In keeping with the geneology theme, the parent node of a parent node is a grandparent and the sibling of a parent node is an uncle.

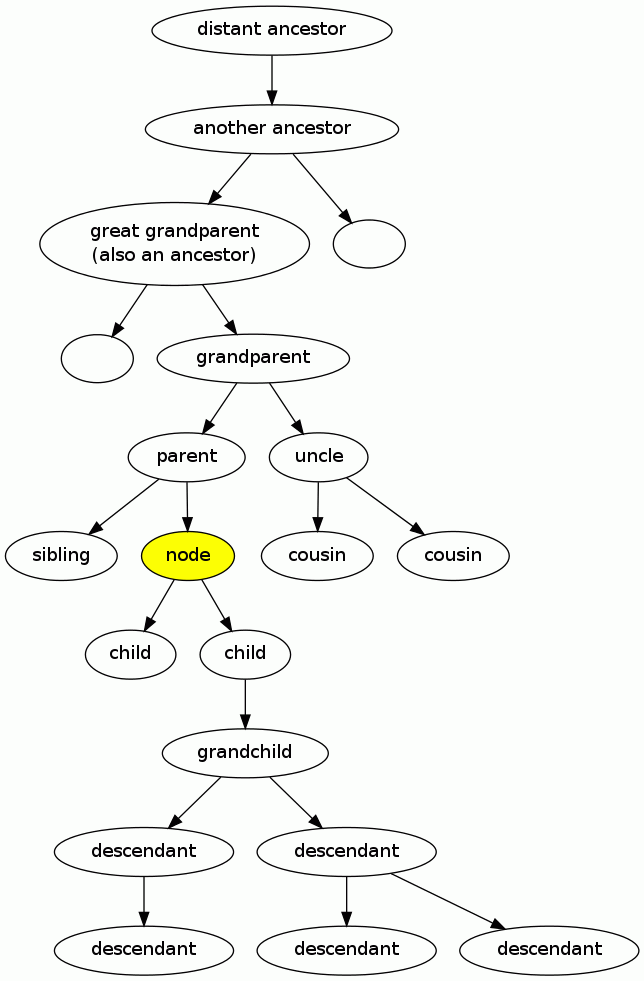
Case-by-case analysis:

1. node is root: relabel node black and return
2. parent is black: return
3. parent and uncle are both red: relabel parent and uncle black and relabel Grandparent as red. Repeat with Grandparent node
   • if parent was red, grandparent must have been black
   • this is the only recursive step, which may propagate color changes up to the root, giving O(log N) color changes.
4. parent is red but uncle is black and node is left child of parent but parent is right child of grandparent or node is right child, but parent is left child (left-right or right-left cases): rotate so node is parent of original parent and original parent is child of node and proceed to case 5 setting node to original parent.
   • the grandparent must be black since it has a red child
   • the sibling of the node (which may be a synthetic leaf) must be black since it's the child of a red node.
5. node is left child of parent and parent is left child of grandparent or node is right child and parent is right child (left-left or right-right cases): relable parent black and grandparent red, then rotate parent to grandparent position and return.

2-3 Tree (Preview)

Only a few minutes left, just time enough for a quick preview of the 2-3 tree.

• a 2-3 tree is a search tree, but it is not a binary search tree
• each node has one or two keys
• each interior node has two or three children (two if it has one key, three if two keys)
• all leaf nodes are at the same height
• nodes are visited in a modified inorder traversal:

  visit(node->left)
  process(node->k1)
  visit(node->middle)
  process(node->k2);
  visit(node->right)
  	  

Insertion

Inserting a key occurs at a leaf node. If the leaf node only has one key, the new key is added in position 1 (with the original key shifted from position 1 to position 2) or position 2.

If the leaf node already has two keys, the middle of the three keys is selected as a root of a three-node mini-tree. The rootlet is passed up to its parent.

When an interior node inserts a new key into one of it's leaf descendants, it is returned either null meaning the insert has occurred, a single-key node representing the modified subtree.

This is fairly straight-forward, but there are a lot of fiddly bits to keep track of in several cases.

More on this in the next lecture.

Deletion

Deletion is similar and similarly messy. Left as an exercise for the reader.