Problem

Using our previous CSS552 ray tracing system, when we compute visibility for a single ray we have to do intersection test for each geometry. Each ray has an O(n) performance. In order to compute visibilities for all rays, we are looking at O(i*j*n) where we have i * j pixels.

Solution

I looked into acceleration structure: bounding volume hierarchy (BVH) and implemented it. According to my result, for a scene contains 75 spheres, it will take about 32 seconds to render without any acceleration structure while it will take 1.6 seconds to render using BVH.

Implementation

There are three parts.

1. Bounding Volume

2. Tree Construction

3. Tree Traversal

1. Bounding Volume:

I used Axis aligned bounding box (AABB) with min and max point implementation.

Below is a sample code

public class AABB
{
   Vector3 mMin;
   Vector3 mMax;

   public AABB(Vector3 min, Vector3 max){…}
}

2. Tree Construction:

I implemented top down tree construction. We start out by bounding all geometry set as root. Next, we use a reference axis to rearrange the order of the geometry set and partition them into two subsets as right and left children. In my implementation, I used local axis as my reference axis. It is also world axis because AABB is aligned with world axis. For partition point, I used objects median. Then, we keep doing the rearrangement and partition recursively until the number of objects in geometries hit certain threshold. I used 10% of the amount of all geometries as my threshold.

Below is a sample code

private void BVHBuild(BVHNode treeNode, List<RTGeometry> objects)
{
   treeNode.BoundingBox = ComputeBoundingVolume(objects); //Bound all the objects in an AABB

   if (objects.Count() <= mMinNumObj)
   {
          treeNode.GeomList = objects;
   }
   else
   {
          int splitIndex =
                RearrangeAndPartitionObject(treeNode.BoundingBox, ref objects);

          BVHBuild(treeNode.Left, ListSubSet(objects, 0, splitIndex));
          BVHBuild(treeNode.Right, ListSubSet(objects, splitIndex, objects.Count()));
   }
}

3. Tree Traversal:

I chose depth first search DFS as my traversal method. We start by checking the root/current node bounding volume intersection. If it does not intersect the bounding volume, then we can skip the rest of test. If it does intersect current node’s bounding volume, then we go deeper down the tree. When we reach the leaf, we do intersecting test for all geometries in this leaf.

Below is a sample code

public bool Traversal(Ray ray, IntersectionRecord rec, int exceptGeom)
{
   // Check ray-bounding volume intersection
   float enterDistance, outDistance;
   if (!RayIntersectAABB(ray, out enterDistance, out outDistance))
          return false;

   if (IsLeaf()) //Base
   {
          bool result = FindIntersectionGeom(ray, rec, exceptGeom);
          return (result && rec.HitDistance >= enterDistance && rec.HitDistance <= outDistance);
   }

   //Depth First Search
   bool rightResult, leftResult;
   rightResult = this.mRight.Traversal(ray, rec, exceptGeom);
   leftResult = this.mLeft.Traversal(ray, rec, exceptGeom);

   return rightResult || leftResult;
}

Result

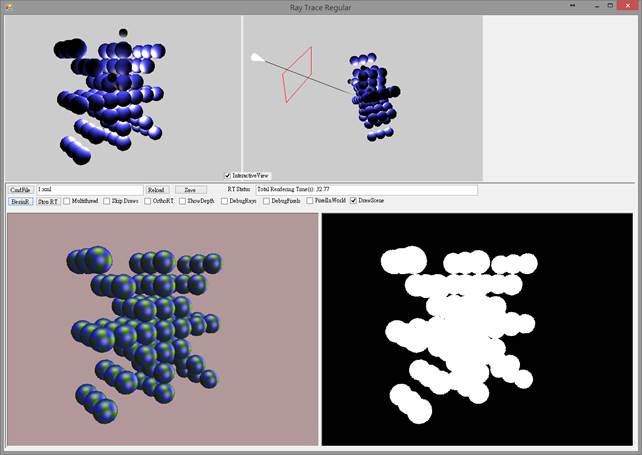
Test 1: 75 Spheres

Without acceleration structure: 32.77 sec

1Regular

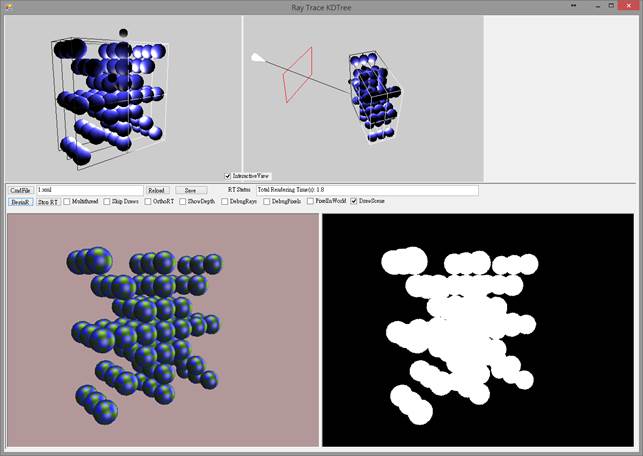
With KD-Tree: 1.8 sec

1KDTREE

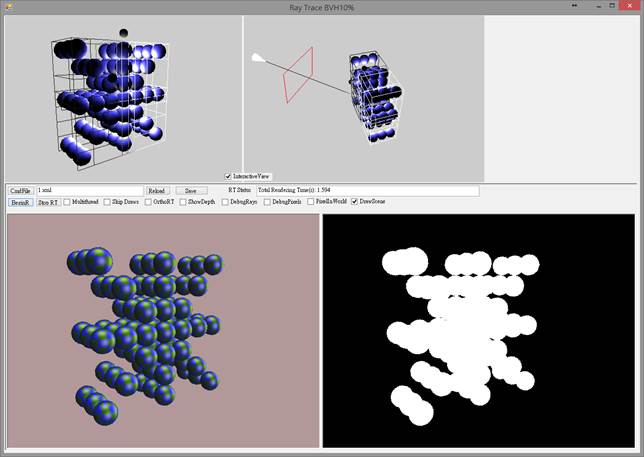
With bounding volume hierarchy: 1.594 sec

1BVH10%

References

James H. Clark. 1976. Hierarchical geometric models for visible surface algorithms. Commun. ACM 19, 10 (October 1976), 547-554. http://doi.acm.org.offcampus.lib.washington.edu/10.1145/360349.360354

Goldsmith, J.; Salmon, J., "Automatic Creation of Object Hierarchies for Ray Tracing," Computer Graphics and Applications, IEEE , vol.7, no.5, pp.14,20, May 1987
http://ieeexplore.ieee.org.offcampus.lib.washington.edu/stamp/stamp.jsp?tp=&arnumber=4057175&isnumber=4057168

Timothy L. Kay and James T. Kajiya. 1986. Ray tracing complex scenes. SIGGRAPH Comput. Graph. 20, 4 (August 1986), 269-278. http://doi.acm.org.offcampus.lib.washington.edu/10.1145/15886.15916

van den Bergen, Gino. “Efficient Collision Detection of Complex Deformable Models Using AABB Trees,”Journal of Graphics Tools, vol. 2, no. 4, pp. 1–14, 1997. http://knight.temple.edu/~lakamper/courses/cis350_2004/etc/jgt98deform.pdf

Amy Williams, Steve Barrus, R. Keith Morley, and Peter Shirley. 2005. An efficient and robust ray-box intersection algorithm. In ACM SIGGRAPH 2005 Courses (SIGGRAPH '05), John Fujii (Ed.). ACM, New York, NY, USA, , Article 9 . http://doi.acm.org/10.1145/1198555.1198748

J. Mahovsky and B. Wyvill. “Fast Ray-Axis Aligned Bounding Box Overlap Tests with Plücker Coordinates.” journal of graphics tools 9:1 (2004), 35–46.