See Website for Due Date

ENGR 100 Assignment 3. Height Calculation

Three spotters will determine the azimuthal angle of the highest point of a rockets flight path.  If the distance between the spotters is known, then the height of the rocket may be calculated.  The geometry of the height calculation appears in Figure 1.

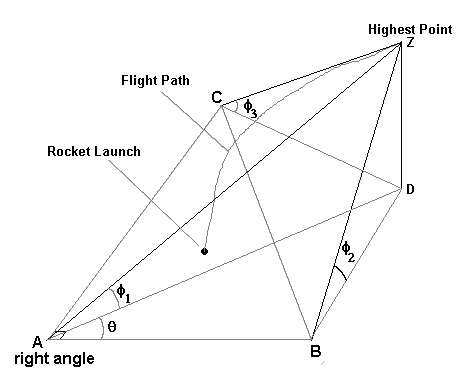
Figure 1 Three dimensional geometry for determining the
maximum height of a rockets flight path. Points
A, B, C and D are on the ground, Z is the highest point.

The spotters will stand at points A, B and C.  Point D is on the ground directly below the highest point Z of the flight path.  The location of point D is, of course, unknown before the launch.  The line segments AB, AC and BC will be marked off on the ground, and are considered known values for the calculation.  The azimuthal angles f₁, f₂, f₃ are measured from the horizontal directly upwards to the highest point.  Three independent azimuthal angles are required to determine the absolute position of an object in three dimensions. 

We must apply the methods of trigonometry to solve for the height.  The geometry of the problem is somewhat challenging, but I invite you to try and derive the system of equations that must be solved to get the height on your own!  In the meantime, here is the system of equations:

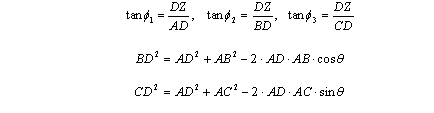
The system contains five equations and five unknowns.  The unknowns are the line segments AD, BD, CD and DZ (which is the height) and the angle q.  This is not a simple system of linear equations that you might have learned to solve in an algebra course.  This is what is called a “non-linear” system and must be solved with more advanced methods.  Don’t get discouraged!  Computers don’t care if the system is “non-linear.” They will solve it anyway.

After a little substitution and re-arranging, the equations can be written as:

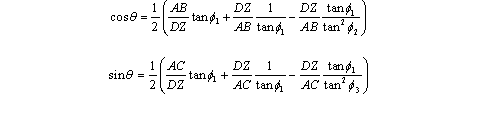
The system has been reduced to two equations and two unknowns.  However, we need one more constraint in order to solve it: a trigonometric identity.

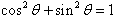
Now we can enter these equations into MS Excel and solve for the maximum height.

Note:  You can download the Excel Spreadsheet from the website or build your own.  Click on the link, then do File/Save.  Then close the browser and open the file using EXCEL.

Assignment:

Now let’s set up the solver.  Go to the Tools menu and click on Solver (sometimes this feature is not available and must be added).  The window Solver Parameters, as seen in Figure 3, should come up. Click on the button to the right of the Set Target Cell input box.  Click on cell A20, then click on the button next to the input box.  You have set the target cell and should return to the window shown in Figure 3.  On the line that starts Equal To: select Value of: and enter 1. By Changing Cells: select cell B13.  This is the cell that contains the initial guess.  One more additional constraint is helpful for obtaining realistic solutions.  In Subject to the Constraints: click the Add button.  Create the additional constraint that the height must be greater than 10 ft.  This is because sometimes the solver gets lost!  There are many mathematical solutions to problems like this one, including solutions that give a negative height!  Excel doesn’t know that the surface of the Earth tends to be an impediment to rocket flight!  Click OK and return to the Solver Parameters window.  Now you are ready to click Solve.  Solver will return a message that says it either found a solution or it didn’t.  Sometimes, even with all the constraints that are given, solver still can’t find a feasible solution.  Usually this is because the initial guess was too far off.  Give another initial guess and try again.  If it does find a solution it will spit out the value DZ in cell B13.

Figure 3 Solver Parameters window

Several students are launching a Big Daddy rocket.  Ann is spotting from point A, Bill is spotting from point B and Carl from point C.

 1. Ann reports 25º, Bill reports 29º and Carl 18º.

a. Put in an initial guess DZ = 50 ft and run the solver. DZ = _____________.

b. Put in an initial guess DZ = 900 ft.  What is DZ now? DZ = ____________.

Notice the difference?  This is because there are many solutions to the problem.  The solver searches for the “closest” solution.  Even though we have constrained it to positive values, it will still occasionally show another solution that probably is not the real solution.  To check this we can calculate the line segments AD, BD and CD.  Try to calculate these line segments from the equations given above.  Notice that CD is well over 1000 ft!  Is this reasonable?  The rocket likely didn’t travel more than 1000 ft horizontally in any direction.  It is safe to throw out this solution and use the previous one.

2. Fill in the following table by calculating the maximum height with the solver.  Check to see if there are other solutions that may be more reasonable.

Bonus Question. On one fateful flight, Ann reports an angle of 90º.  Bill reads 33º and Carl was tying his shoe and didn’t get a reading.  Can you still find the maximum height?  If so, what is it?  Explain how you got your answer.

Creating EXCEL File

Create an Excel spreadsheet that looks like Figure 2.  The format of the cells and units is different from what you would typically use for creating tables and plots.  The known line segment lengths are entered in rows 3 – 5.  The angles f₁, f₂, f₃  measured in degrees by the spotters are entered in column B rows 8-10.  We must convert from degrees to radians.  The conversion factor is 180° = p radians.  In column D row 8 enter:

 = Pi()/180*B8

 Notice how Excel recognizes the constant p.  Open and close parentheses must follow a capital P and lower case i.  Fill down for rows 9 and 10.

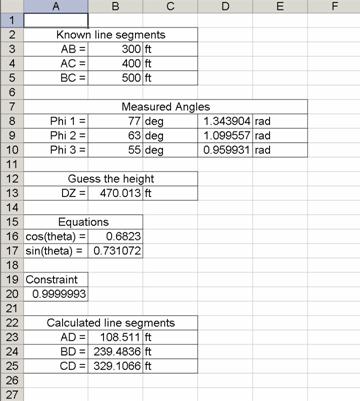
Figure 2 Excel spreadsheet

Excel has a solver routine that requires an initial guess for the height DZ.  For now just enter any value in cell B13.  In B16 and B17 enter the equations for cosq and sinq as given above.  However, you must enter the cell location (column and row) for each value. Excel will not recognize characters like f₁ and AB.  Enter the constraint equation in cell A20:

= B16^2+B17^2