



MGJ 27 OCT 96
PURPOSE
The purpose of this exercise is to determine the
effect of cyclic loads on the long-term behaviour of structures
and to determine the fatigue lives (Nf) as functions of uniaxial
tensile stress for an aluminum alloy. Axial fatigue tests are
used to obtain the fatigue strength of materials where the strains
are predominately elastic both upon initial loading and throughout
the test.
EQUIPMENT
Reduced gage section tensile specimens of 6061-T6 aluminum
Tensile test machine with grips, controller, and
data acquisition system
PROCEDURE
Measure the diameter, d, of the gage section of the specimen
to 0.02 mm.
Calculate the maximum, Pmax, and minimum, Pmin, loads for the test based on the desired maximum and minimum stresses (Note: P = s*A = s * (pd2/4) . Since, these tests are being conducted in tension only, the stress ratio, R, is chosen to be close to but not exactly zero such that R=0.1. Thus, smin=R*smax where smax is the desired maximum stress.
Calculate the mean load as Pm=(Pmax +Pmin)/2.
Calculate the load amplitude as Pa=(Pmax
-Pmin)/2.
Zero the load output (balance).
Set the maximum load limit at ~5 kN during the specimen installation and activate the limit detect for actuator off.
Do not set the minimum load limit during specimen installation
Activate load protect (~0.1 N) on the test machine to prevent
overloading the specimen during installation.
Install the top end of the tensile specimen in the top grip of the test machine while the test machine is in displacement control.
Install the bottom end of the tensile specimen in the lower grip of the test machine.
Set the maximum load limit at ~0.5 kN greater than Pmax and activate the limit detect for actuator off.
Set the minimum load limit at -0.2 kN and activate the limit detect for actuator off.
Deactivate load protect.
Activate load control by going to this control mode immediately,
On the test machine, zero the cycle counter for the total count.
In load control adjust the setpoint in increments of not greater than 1kN to achieve the mean load, Pm.
Select the waveform as sine wave and input an initial frequency of 1 Hz
Input the load amplitude, Pa.
Activate amplitude control to ensure that the loading envelope maintains its integrity during the course of the test.
Initiate the data acquisition and control program (if desired).
Enter the correct file name and specimen information as required.
Initiate the test sequence via the computer program otherwise activate the test via the front control panel.
After the test has been running for 30-60 s, increase the frequency in 1 Hz increments up to a maximum of 15 Hz.
Activate event detector 1 for break detect but no action.
Continue the test until specimen fracture (or the break detect).
Record the number of cycles on the cycle counter at the end
of the test.
* REFERENCES
Annual Book or ASTM Standards,
American Society for Testing and Materials, Vol. 3.01
E466 Standard Practice for Conducting Constant Amplitude Axial Fatigue Tests of Metallic Specimens
E468 Standard Practice for Presentation of Constant Amplitude Fatigue Test Results for Metallic Specimens
RESULTS
Fatigue test results may be significantly influenced by the properties
and history of the parent material, the operations performed during
the preparation of the fatigue specimens, and the testing machine
and test procedures used during the generation of the data. The
presentation of the fatigue test results should include citation
of the basic information on the material, the specimens, and testing
to increase the utility of the results and to reduce to a minimum
the possibility of misinterpretaion or improper application of
the results.
Tabulate your results in the Table 1, comparing your results to
the control data generated for this same aluminum under uniaxial
tensile fatigue conditions.
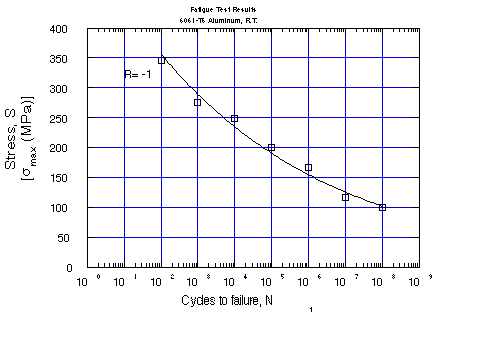
Plot your test results as maximum stress, smax
, versus log of cycles to failure, Nf
in Figure 1. Note that a log scale is used for Nf so there is
no need to compute log Nf.
Answer the following questions on the Worksheet, turning this
in as the In-class Lab report.
MGJ 27 OCT 96
NAME______________________________________DATE______________
EQUIPMENT IDENTIFICATION______________________________________
1) Tabulate the following mechanical properties from your
tensile test results.
6061- T6 Aluminum
Selected Mechanical Properties (R.T.)
| E (GPa) | ||
|
|
| |
|
|
| |
| % elongation |
| Specimen diameter, d (mm) | ||
| Gage section area, A=pd2/4 (mm2) | ||
| Stress ratio, R | ||
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
|
3) Tabulate your test results and compare them to the control
data for this material.
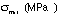 | 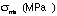 |
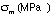 | 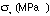 | ||
| Suts= | |||||
4) cont'd
5) Do your test results agree with the control (or previous
test) results. If so, why? if not, why not? Would you expect
fatigue failures to have little or much scatter? Does it seem
reasonable to try to fit a single curve through the data?
6) Examine the fracture surface of the specimen. Given
that the maximum load in the fatigue test was less than the yield
load for material (as determined from the monotonic tensile test),
discuss how fatigue can occur given that the loading was in the
elastic range. Where do the fatigue cracks initiate from? Is
surface condition important? How would you design components
to minimize fatigue failures?
7) Fatigue can be analyzed from a fracture mechanics standpoint.
If the stress intensity factor solution for this case can be
approximaed as 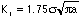 , determine the critical
crack length at fracture such that
, determine the critical
crack length at fracture such that 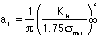 for
your result (Note KIc=35 MPaÃm).
Compare calculated af to the actual af
measured on the fracture surface. Are they similar? Why
or why not? Finally, assuming ai=0.1 mm and
da/dN =C(DK)m
(Note: a has units of metres, s
has units of MPa, F=1.75, m=3.59 and C=1.6 X 10-11
with units to give da/dN in m/cycle), calculate the cycles
to failure from tensile crack initiation to final fracture using
the relation:
for
your result (Note KIc=35 MPaÃm).
Compare calculated af to the actual af
measured on the fracture surface. Are they similar? Why
or why not? Finally, assuming ai=0.1 mm and
da/dN =C(DK)m
(Note: a has units of metres, s
has units of MPa, F=1.75, m=3.59 and C=1.6 X 10-11
with units to give da/dN in m/cycle), calculate the cycles
to failure from tensile crack initiation to final fracture using
the relation: 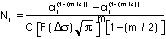 . Compare the Nf
for crack propagation to the total Nf for
the test. Is crack propagation a significant part of the total
fatigue life?
. Compare the Nf
for crack propagation to the total Nf for
the test. Is crack propagation a significant part of the total
fatigue life?