Rough Sketch of Gödel Incompleteness (1931) 

In any reasonable FS the following sets are decidable (i.e., there is an effective decision procedure such that, given any putative element x of the set, the procedure will answer whether x does or does not belong to the set):

1. Vocabulary: the vocabulary (broken down into the various categories -- e.g., predicates, variables, etc.)
2. Well-formed-formulas: the set of those sequences of elements of the vocabulary that are wffs of the FS
3. Proofs: the set of those sequences of wffs that constitute proofs in the FS
4. Prf-Thm: the set of pairs (proof, theorem) where the proof proves the theorem.

Background :

(1) Any decidable set can be effectively represented in arithmetic, in the sense that there is a 1-1mapping between the elements of the set and the natural numbers such that
(a) Given any element X of the set one can effectively determine its representing number (called its Gödel number --"gn X").
(b) Given any number one can effectively determine whether it is the gn of some element of the set and, if so, of which element it is the gn.
(c) The set of representing numbers ("gns") is itself a decidable set of numbers.

(2) Any decidable numerical relation (i.e., one such that the numbers satisfying the relation form a decidable set) can be expressed in arithmetic, in the sense that there is a formula of arithmetic that is provable for numerals when the corresponding numbers satisfy the relation, and whose negation is provable otherwise.

Scope: We consider any reasonable first order theory AR of arithmetic; i.e., one that is rich enough ("sufficiently rich") to represent all the natural numbers and the usual relations of "=", "<", and the operations of "+" and ".". We assume that we have as constants ("name letters"), either as primitive members of the vocabulary or as introduced by definitions, all the usual numerals 1, 2, 3, ... . (We will use bold face to indicate expressions in the vocabulary of AR.)

Where m and y are variables ranging over the natural numbers consider the relation W(m, y) that holds between the numbers m and y just in case

(a) m = the gn of a wff Fx1 with x1 free and
(b) y = the gn of a proof of Fm.

Note that this relation is decidable; i.e., that the set of pairs of numbers (m, y) such that W(m, y) is a decidable set.
Hence by (2) above we can express the relation W(m, y) in AR, say, by the formula W(m, y)

Let (*) be the formula (x2)~W(x1, x2) and let m = gn(*).

Let (**) be the sentence (x2)~W(m, x2) obtained from (*) by substituting numeral m for free variable x1.

Note that W(m, x2) iff m = gn of a wff Fx1 with x1 free and x2 = the gn of a proof of Fm. But m = gn(*) = gn of (x2)~W(x1, x2), which has x1 free. Hence,

      W(m, x2) iff m = gn((x2)~W(x1, x2)) and

x2 = gn of a proof of (x2)~W(m, x2); i.e., x2 = gn of a proof of (**).

Thus (**) codes for "there is no proof of (**)"; i.e. (**) says that (**) is not a theorem. Recall that a FS is negation complete just in case for every closed formula either it or its negation is provable.

Gödel's (First) Incompleteness Theorem. If AR is consistent, then it is not negation complete;
in particular neither (**) nor ~(**) is a theorem of AR.

Proof: If AR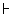 (**) then let x = gn of a proof of (**). Then W(m, x). Since the relation W is decidable, AR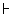W(m, x). But (**)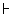~W(m, x). Thus AR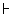(**) implies that AR is inconsistent.
If AR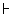~(**), then AR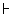"(**) is a theorem" hence AR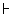 (**), which again would make AR inconsistent. (This half of the proof is actually a little more complicated when set out rigorously.)

Notice that (**) expresses some perfectly ordinary numerical statement. Hence, intuitively, it is either true of the numbers, or false. That is, either (**) is true in arithmetic or ~(**) is true. (Indeed, (**) would seem to be true -- because it is unprovable.) Hence we have

Corollary . Any reasonable system of arithmetic contains some true arithmetical statement
that cannot be proved in the system.

Question to think about: When would we want to say that a predicate is "definable"? What, then, do we want to say about the definability of the truth predicate ("is true") in the light of the Corollary?

Recall that the set of proofs is decidable, as is the relation between a proof and what it proves. Hence we can express the consistency of arithmetic in any reasonable system of arithmetic, since consistency just says that something (e.g., 0=1) is not provable. Let Cons (AR) be the expression in AR of the consistency of AR.

Gödel's Second Incompleteness Theorem.
If AR is consistent then Cons(AR) is not provable in AR.

You can get a flavor of the proof here if you recall that (**) codes for "there is no proof of (**)". Hence, if we can carry out in arithmetic the proof of Gödel's first theorem above we would prove [Cons (AR) --> (**)] in AR. Hence if Cons(AR) were provable in AR, then we would have a proof in AR of (**), contrary to the first incompleteness theorem.

Finally, there is a related result due to Alonzo Church.

Church's Theorem. Arithmetic is undecidable; i.e., there is no decision procedure that can tell
for an arbitrary sentence of arithmetic whether or not it is provable.

More generally, there is no effective decision procedure for the theorems of predicate logic, and this remains true even if we restrict ourselves to the logic of two place predicates.
Since AR would be decidable if it were consistent and negation complete, Church's Theorem is another route to the incompleteness of AR.

See the article Kurt Gödel in the Stanford Encyclopedia of Philosophy for an account of Gödel's original proofs and their background (http://plato.stanford.edu/entries/goedel/).