The three axiom
schemas below, together with the one rule of inference, constitute a
complete set of axioms for sentential logic. The Greek letters stand
for any sentence in the system.
Ax 1 (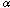
 (
(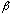

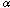 ))
))
Ax 2 (((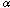
 (
(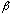

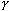 ))
)) ((
((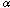

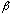 )
) (
(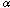

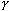 )))
)))
Ax 3 ((~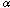
 ~
~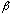 )
) ((~
((~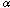

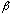 )
)
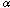 )))
)))
Rule of Inference (Modus Ponens): 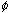 , (
, (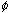

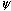 )
)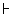
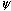
(To make life a
little easier I will omit outside parentheses below.)
T1. 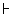 P
P P
P
- P
 ((P
((P P)
P) P)
Ax1
P)
Ax1
- ((P
 ((P
((P P)
P)  P ))
P )) ((P
((P  (P
(P P))
P)) (P
(P  P ))
Ax2
P ))
Ax2
- (P
 (P
(P P))
P)) (P
(P  P )
1, 2 MP
P )
1, 2 MP
- P
 (P
(P P)
Ax1
P)
Ax1
- P
 P
3, 4 MP
P
3, 4 MP
I. Proof that 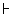 (~P
(~P P)
P) P
P
1. (~P ~P)
~P) ((~P
((~P P)
P) P))
Ax 3
P))
Ax 3
2. ~P ~P
Thm 1
~P
Thm 1
3. (~P P)
P) P
1,2 MP
P
1,2 MP
II. Proof that
{(P Q), (Q
Q), (Q R)}
R)} 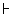 (P
(P R)
R)
1. (Q R)
R) (P
(P (Q
(Q R))
Ax 1
R))
Ax 1
2. Q R
Assumption
R
Assumption
3. P (Q
(Q R)
1,2 MP
R)
1,2 MP
4. ((P (Q
(Q R))
R)) ((P
((P Q)
Q) (P
(P R))
Ax 2
R))
Ax 2
5. (P Q)
Q) (P
(P R)
3,4 MP
R)
3,4 MP
6. P Q
Assumption
Q
Assumption
7. P R)
5,6 MP
R)
5,6 MP
III. Proof that {P, ~P} 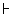 Q (i.e., that anything follows
from a contradiction; sometimes called the principle of explosion))
Q (i.e., that anything follows
from a contradiction; sometimes called the principle of explosion))
1. (P (~Q
(~Q P))
Ax
1
P))
Ax
1
2. P
Assumption
3. (~Q P)
1,2 MP
P)
1,2 MP
4. ~P (~Q
(~Q ~P)
Ax 1
~P)
Ax 1
5. ~P
Assumption
6. ~Q ~P)
4,5 MP
~P)
4,5 MP
7. (~Q ~P)
~P) ((~Q
((~Q P)
P) Q))
Ax 3
Q))
Ax 3
8. (~Q P)
P) Q
6, 7 MP
Q
6, 7 MP
9. Q
3,8 MP
IV. Proof that
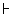 ~ ~P
~ ~P P
P
1. (~P ~ ~P)
~ ~P) [(~P
[(~P ~P)
~P) P]
Ax 3
P]
Ax 3
2. ((~P ~ ~P)
~ ~P) [(~P
[(~P ~P)
~P) P])
P])
([(~P ~ ~P)
~ ~P) (~P
(~P ~P)]
~P)] [(~P
[(~P ~ ~P)
~ ~P) P])
Ax 2
P])
Ax 2
3. [(~P ~ ~P)
~ ~P) (~P
(~P ~P)]
~P)] [(~P
[(~P ~ ~P)
~ ~P) P]
1,2 MP
P]
1,2 MP
4. (~P ~P)
~P) [(~P
[(~P ~
~P)
~
~P) (~P
(~P ~P)]
Ax 1
~P)]
Ax 1
5. ~P ~P
Thm
1
~P
Thm
1
6. (~P ~ ~P)
~ ~P) (~P
(~P ~P)
4, 5 MP
~P)
4, 5 MP
7. (~P ~ ~P)
~ ~P) P
3,6 MP
P
3,6 MP
8. ~ ~P (~P
(~P ~ ~P)
Ax 1
~ ~P)
Ax 1
9. ~ ~P P
8,7 II (above)
P
8,7 II (above)
Corollary of IV. ~~P 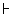 P
(Double Negation, Part 1)
P
(Double Negation, Part 1)
Proof: Given ~~P, use that with 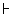 ~~P
~~P P and MP to infer P.
P and MP to infer P.
V.
Proof that P Q, ~Q
Q, ~Q 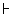 ~P
(Modus Tollens)
~P
(Modus Tollens)
1. ~ ~P P
Thm (IV, above)
P
Thm (IV, above)
2. P Q
Assumption
Q
Assumption
3. ~ ~P Q
1,2 II (above)
Q
1,2 II (above)
4. (~ ~P ~Q)
~Q) [(~ ~P
[(~ ~P Q)
Q) ~P]
Ax 3
~P]
Ax 3
5. ~Q (~ ~P
(~ ~P ~Q)
Ax 1
~Q)
Ax 1
6. ~Q
Assumption
7. (~ ~P ~Q)
5,6 MP
~Q)
5,6 MP
8. (~ ~P Q)
Q) ~P
4,7 MP
~P
4,7 MP
9. ~P
3,7 MP
VI. Proof that P 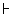 ~ ~P
(Double Negation, Part 2)
~ ~P
(Double Negation, Part 2)
1. (~~~P ~P)
~P) [(~~~P
[(~~~P P)
P) ~~P]
Ax 3
~~P]
Ax 3
2. ~~~P ~P
Thm IV (above)
~P
Thm IV (above)
3. (~~~P P)
P) ~~P
1, 2 MP
~~P
1, 2 MP
4. P
Assumption
5. P (~~~P
(~~~P P)
Ax 1
P)
Ax 1
6. ~~~P P
4, 5 MP
P
4, 5 MP
7. ~~P
3,6 MP
Thus
the rules of MP, DN and MT all hold. If we had
the
resources for conditional proof we would have all the machinery for a
natural
deduction system. What we require is the following result.
(Weak) Deduction Theorem (Herbrand, 1930): If 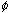
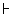
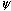 ,
then
,
then 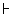 (
(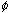

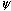 ).
).
(It is not hard to show this by induction on the number of steps in the
derivation of 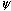 from
from 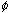 .
.
See Mendelson, p. 32.)