Sample Problem 4 in ch. 4-3, pp.59-60 demonstrates a projectile motion problem, where the original angle is known. Problems 9 (p.69) and 28 (p.71) at the end of ch. 4 are similar, but without the original angle. I find myself subtracting sec^2 (theta) from tan (theta). Do you have any hints to get past that step?
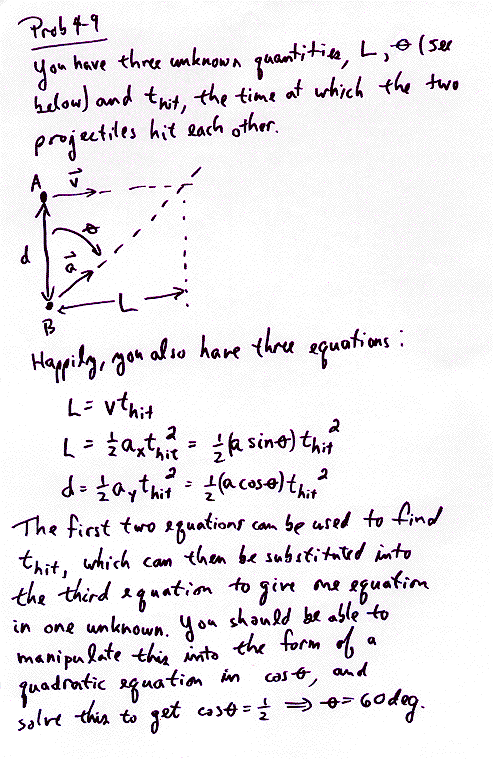
Well, I'm not really sure how you attacked these problems to get to that particular trig problem, but I can tell you how I would attack those two probs. First, Prob.4-28 is very similar to the type of projectile problem that was discussed (and demo'd) in class last week -- you should take a look at the derivations in section 4-3, especially the steps leadin gup to Eq.24 -- I think that Eq.24 can be used directly to solve Prob.4-28. On the other hand, Prob.4-9 is a bit more interesting. My first stab at a solution (outlined below) works fine, but is a little complicated. Let me know if you find a more direct way to solve for the desired angle.
