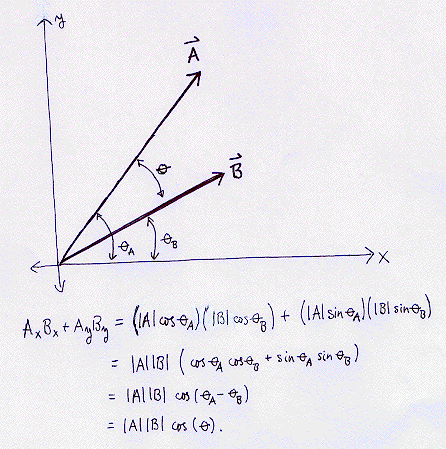Pp. 43-44 in RHK introduces the dot product. I can understand, that the dot product of vector components in the same direction or of parallel vectors is simply the product of their magnitudes. And that the dot product of non parallel vectors is the sum of each of their dot products in the x,y and z directions. But I only understand that this is so by definition. Is there a graphical interpretation of the dot product, so that I can see what it looks like?
The geometric explanation that you are looking for is in Fig.16 of RHK, but is a bit obscured by the complexity of the figure. Consider the special case where one of the two vectors is a unit vector. See below:

So, the dot product of the vectors A and u is is simply the magnitude of the projection of vector A onto the direction of vector u. If the direction of the two vectors are perpendicular, then the dot product will be zero. If the second vector were not a unit vector, then the dot product is equal to the projection of the first vector onto the direction of the second, multiplied by the magnitude of the second vector. Of course, this doesn't tell you *why* the sum of the product of the components is equal to ABcos(theta). See below: