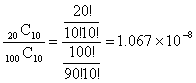Homework 3 Solutions

Page 111 #10

This is classical probability, since each combination is equally likely.

Page 112 #14

P(selecting a number > 1000) = (6296-1000)/6296 = .841

Page 112 #20

P(voter chosen at random is not between 25 and 34 years old) = (193.7 – 40.1)/193.7 = .793

Page 112 #22

P(offspring has same coloring as one of parents) = 8/16 = .5

Page 113 #26

P(worker chosen at random not in agric., forestry or fisheries) = (127,900 – 3,592)/127,900 = .972

Page 119 #8

These events are independent, since the two balls have an equal chance of being chosen (assuming the balls were mixed after replacing the first).

Page 120 #12

Let A = the event that adults think race relations have improved since the death of MLK

Let B = the event that adults say civil rights have progressed too slowly

P(A) = .6

P(B|A) = .4

(a) P(A and B) = P(A) P(B|A) = (.6)(.4) = .24

(b) P(B’|A) = 1 - P(B|A) = .60

Page 122 # 18

Let O = the event that a person has blood type O⁺

P(O) = .38

(a) P(all three people have O⁺) = .38³ = .055

(b) P(none have O⁺) = (1 - .38)³ = .62³ = .238

Page 123 #24

Let A = the event a person is infected

Let B = the event a person tests positive

P(A) = 1/200

P(B|A) = .80

P(B|A’) = .05

We can also write:

P(B’|A) = .20

P(B’|A’) = .95

Page 129 #10

Not mutually exclusive, because it is possible that some people in the population of 18 to 24 year olds earn $20,000 to $29,999.