Abstract: That cuckoo eggs were peculiar to the locality where found was already known in 1892. A study by E.B. Chance in 1940 called The Truth About the Cuckoo demonstrated that cuckoos return year after year to the same territory and lay their eggs in the nests of a particular host species. Further, cuckoos appear to mate only within their territory. Therefore, geographical sub-species are developed, each with a dominant foster-parent species, and natural selection has ensured the survival of cuckoos most fitted to lay eggs that would be adopted by a particular foster-parent species.
Image: Boxplot of Cuckoo Eggs by Other Bird Species
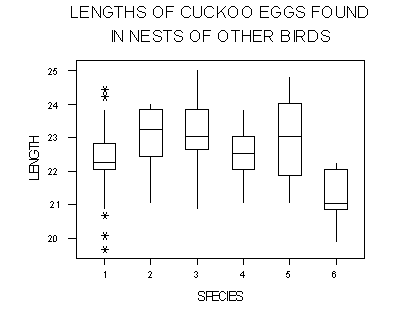
Number of cases: 115
Variable Names:
- 1. MDW PIPIT: Meadow Pipit
- 2. TREE PIPIT: Tree Pipit
- 3. HDGE SPRW: Hedge Sparrow
- 4. ROBIN: Robin
- 5. PIED WTAIL: Pied Wagtail
- 6. WREN: Wren
All data are lengths in millimeters (see table on separate page). For this test, we are comparing average egg lengths among the host species type.
|
egg |
MDW PIPIT |
TREE
PIPIT |
HDGE SPRW |
PIED
ROBIN |
WTAIL |
WREN |
|
1 |
19.65 |
21.05 |
20.85 |
21.05 |
21.05 |
19.85 |
|
2 |
20.05 |
21.85 |
21.65 |
21.85 |
21.85 |
20.05 |
|
3 |
20.65 |
22.05 |
22.05 |
22.05 |
21.85 |
20.25 |
|
4 |
20.85 |
22.45 |
22.85 |
22.05 |
21.85 |
20.85 |
|
5 |
21.65 |
22.65 |
23.05 |
22.05 |
22.05 |
20.85 |
|
6 |
21.65 |
23.25 |
23.05 |
22.25 |
22.45 |
20.85 |
|
7 |
21.65 |
23.25 |
23.05 |
22.45 |
22.65 |
21.05 |
|
8 |
21.85 |
23.25 |
23.05 |
22.45 |
23.05 |
21.05 |
|
9 |
21.85 |
23.45 |
23.45 |
22.65 |
23.05 |
21.05 |
|
10 |
21.85 |
23.45 |
23.85 |
23.05 |
23.25 |
21.25 |
|
11 |
22.05 |
23.65 |
23.85 |
23.05 |
23.45 |
21.45 |
|
12 |
22.05 |
23.85 |
23.85 |
23.05 |
24.05 |
22.05 |
|
13 |
22.05 |
24.05 |
24.05 |
23.05 |
24.05 |
22.05 |
|
14 |
22.05 |
24.05 |
25.05 |
23.05 |
24.05 |
22.05 |
|
15 |
22.05 |
24.05 |
* |
23.25 |
24.85 |
22.25 |
|
16 |
22.05 |
* |
* |
23.85 |
* |
* |
|
17 |
22.05 |
* |
* |
* |
* |
* |
|
18 |
22.05 |
* |
* |
* |
* |
* |
|
19 |
22.05 |
* |
* |
* |
* |
* |
|
20 |
22.05 |
* |
* |
* |
* |
* |
|
21 |
22.25 |
* |
* |
* |
* |
* |
|
22 |
22.25 |
* |
* |
* |
* |
* |
|
23 |
22.25 |
* |
* |
* |
* |
* |
|
24 |
22.25 |
* |
* |
* |
* |
* |
|
25 |
22.25 |
* |
* |
* |
* |
* |
|
26 |
22.25 |
* |
* |
* |
* |
* |
|
27 |
22.25 |
* |
* |
* |
* |
* |
|
28 |
22.25 |
* |
* |
* |
* |
* |
|
29 |
22.45 |
* |
* |
* |
* |
* |
|
30 |
22.45 |
* |
* |
* |
* |
* |
|
31 |
22.45 |
* |
* |
* |
* |
* |
|
32 |
22.65 |
* |
* |
* |
* |
* |
|
33 |
22.65 |
* |
* |
* |
* |
* |
|
34 |
22.85 |
* |
* |
* |
* |
* |
|
35 |
22.85 |
* |
* |
* |
* |
* |
|
36 |
22.85 |
* |
* |
* |
* |
* |
|
37 |
22.85 |
* |
* |
* |
* |
* |
|
38 |
23.05 |
* |
* |
* |
* |
* |
|
39 |
23.25 |
* |
* |
* |
* |
* |
|
40 |
23.25 |
* |
* |
* |
* |
* |
|
41 |
23.45 |
* |
* |
* |
* |
* |
|
42 |
23.65 |
* |
* |
* |
* |
* |
|
43 |
23.85 |
* |
* |
* |
* |
* |
|
44 |
24.25 |
* |
* |
* |
* |
* |
|
45 |
24.45 |
* |
* |
* |
* |
* |
|
Average |
22.29888889 |
23.09 |
23.12142857 |
22.575 |
22.90333333 |
21.13 |
|
SD |
0.920627805 |
0.901427439 |
1.068736545 |
0.684592336 |
1.067618623 |
0.743735744 |
Question:
Assuming the samples of cuckoo lengths are independent, perform three two-sample t-tests on the cuckoo egg length data, using two-tailed tests with a 0.05 level of significance. Choose any samples you wish to compare (later on we will learn how to do Analysis of Variance, in which case all of the samples can be compared at once). Assume unequal variances, but for one of your tests assume both equal and unequal variances. What kind of biological inferences might you make based on all of these tests?
A) Write the null and alternative hypotheses
B) Decide on your sampling distribution and find your rejection regions
C) Calculate your (3) test statistic(s)
In general, H0: mi = mj ; Ha: mi ¹ mj where i,j = 1,2,…6, i ¹ j, 1 refers to the first sample (first column of data) up
through the last column (= 6)
For example, i=1,j=2, then: H0: m1 = m2 ; Ha: m1 ¹ m2
Xbar:1 = 22.30 ; n1 = 45 ; s1
= 0.921
Xbar:2 = 23.09 ; n2 = 15 ; s2
= 0.901
For unequal variances, sxbar1-xbar2 = 0.270; for
equal variances sxbar1-xbar2 = 0.239
For unequal variances t = -2.94; for equal variances
t = -3.31
t0 = +/-2.145 with 14 df (unequal variances)
t0 =
+/-1.96 with 58 df
Description: Prices in cents per pound received by fishermen and vessel owners for various species of fish and shellfish in 1970 and 1980
Number of cases: 14
Variable Names:
1. Type_Fish: Species of fish
2. Price_1970: Price in cents per pound in 1970
3. Price_1980:
Price in cents per pound in 1980
The Data:
|
Type_Fish |
Price_1970 |
Price_1980 |
d |
d2 |
|
COD |
13.1 |
27.3 |
14.2 |
201.64 |
|
FLOUNDER |
15.3 |
42.4 |
27.1 |
734.41 |
|
HADDOCK |
25.8 |
38.7 |
12.9 |
166.41 |
|
MENHADEN |
1.8 |
4.5 |
2.7 |
7.29 |
|
OCEAN
PERCH |
4.9 |
23 |
18.1 |
327.61 |
|
SALMON,
CHINOOK |
55.4 |
166.3 |
110.9 |
12298.81 |
|
SALMON,
COHO |
39.3 |
109.7 |
70.4 |
4956.16 |
|
TUNA,
ALBACORE |
26.7 |
80.1 |
53.4 |
2851.56 |
|
CLAMS,
SOFT-SHELLED |
47.5 |
150.7 |
103.2 |
10650.24 |
|
CLAMS,
BLUE HARD-SHELLED |
6.6 |
20.3 |
13.7 |
187.69 |
|
LOBSTERS,
AMERICAN |
94.7 |
189.7 |
95 |
9025 |
|
OYSTERS,
EASTERN |
61.1 |
131.3 |
70.2 |
4928.04 |
|
SEA
SCALLOPS |
135.6 |
404.2 |
268.6 |
72145.96 |
|
SHRIMP |
47.6 |
149 |
101.4 |
10281.96 |
|
|
|
Sum |
961.8 |
128762.78 |
Decide which kind of test would be appropriate for these data and perform that test. Test for significance at the 0.05 level. What you want to compare is the price of fish in 1970 to the price of fish in 1980. Test the claim that the price of fish increased between the two times.
A) Write the null and alternative hypotheses
B) Decide on your sampling distribution and find your rejection regions
C) Calculate your (3) test statistic(s)
Do a paired t-test.
Utilize the extra columns above to calculate your d’s and d2’s
(see values above) which will help you calculate sd and dbar.
These are the calculated values you need for your
test statistic:
dbar = 68.7 ; sd = 69.44 ; sdbar
= 18.56
t = 3.70 ; t0 = 2.160 (looking at a = 0.05, 13 df)
Reject the null hypothesis, conclude that the prices
have changed for fish in general.