
egrep --color=tty
to test examples of regular expression matching
anbn
for all values of
n
is a context-free language
anbmanbm
for all values of
n
and
m
is
not
a context-free language
anbmcn+m
for all values of
n
and
m
is
context-free because the counter is counting
k = n + m
T
(usually represented by lowercase letters
a,
b,
c,
...)
N
(usually represented by uppercase letters
A,
B,
C,
...)
S
L(G):
set of strings of
terminal
symbols that can be generated from the start symbol by repeated
application of production rules
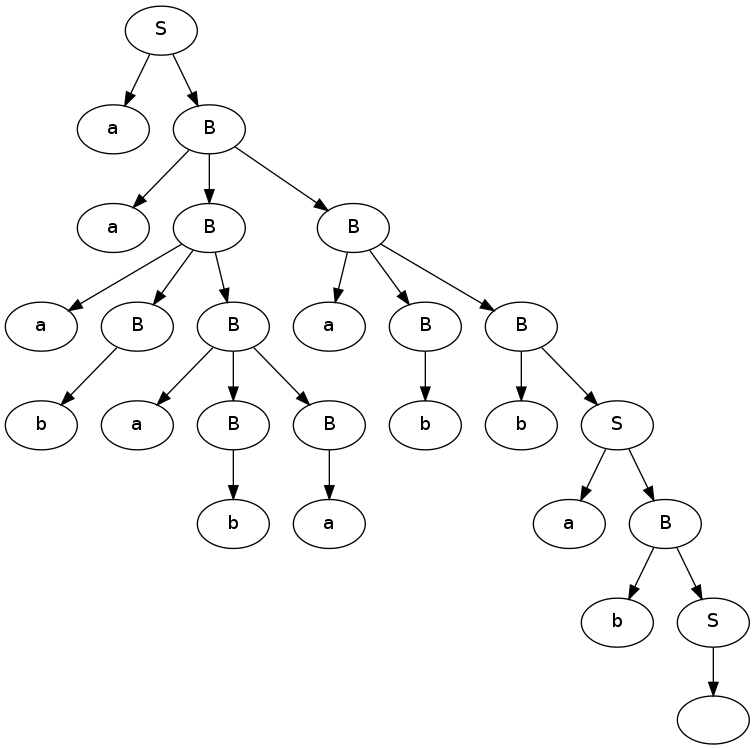
Example 1: palindromes (strings that read the same forwards and
backwards) over the alphabet of terminals
{a, b}.
Generate the string
abaabaaba
given the following grammar:
S → ε
S → a
S → b
s → bSb
S → aSa
aSa → abSba
abSba → abaSaba
abaSaba → abaaSaaba
abaaSaaba → abaabaaba
More compactly:
S → aSa → abSba → abaSaba → abaaSaaba → abaabaaba
Example 2: expressions. Generate the string
number * ( number * id + id ) given the following
grammar (nonterminals are italicized):
expression → expression * expression
expression → expression + expression
expression → ( expression )
expression → id
expression → number
expression
→ expression * expression
→ expression * ( expression )
→ expression * ( expression + expression )
→ expression * ( expression * expression + expression )
→ number * ( expression * expression + expression )
→ number * ( number * expression + expression )
→ number * ( number * id + expression )
→ number * ( number * id + id )
Example 3:
anbmcn+m.
Generate the string
aaabbcccccc:
S → ε
S → aSc
S → T
T → bTC
T → bc
S → aSc → aaScc → aaaSccc → aaaTccc → aaabTcccc → aaabbcccccc
Example 4: balanced parentheses:
S → ε
S → (S)
s → SS
Example 5: equal number of
as
and
bs
(in any order).
Generate the string
aaab abba bbab
S → ε
S → aB
S → bA
A → aS
A → bAA
B → bS
B → aBB
S → aB
aB → aaBB
aaBB → aaaB BB
aaaB BB → aaab BB
aaab BB → aaab aBBB
aaab aBBB → aaab abBB
aaab abBB → aaab abbB
aaab abbB → aaab abba BB
aaab abba BB → aaab abba bB
aaab abba bB → aaab abba bbS
aaab abba bbS → aaab abba bbaB
aaab abba bbaB → aaab abba bbab S
aaab abba bbab S → aaab abba bbab
The grammar keeps track of the balance
as
or
bs
seen so far: every time an
a
is produced, it's either from an
A
(required to balance some
b
to the left)
or it's from a
B
and an additional
B
is added to the derivation string (incrementing the number of
required
bs
We established by example that Context-Free Languages can recognize languages that are proven to be not regular (e.g. palindromes). To show that CFLs are a superset of regular languages, we show that for every regular expression, there is an equivalent CFG construction:
| RE | CFG | |
|---|---|---|
| zero-or-more |
x*
|
A → XA
A → ε
|
| concatenation |
xy
|
A → XY
|
| or |
x|y
|
A → X
A → Y
|
L(G)
expression
→ expression + expression
→ expression * expression + expression
→ id * expression + expression
→ id * id + expression
→ id * id + id
expression
→ expression * expression
→ id * expression
→ id * expression + expression
→ id * id + expression
→ id * id + id
(id * id) + id;
the latter roughly coresponds to
id * (id + id).
An unambiguous grammar for the same language is:
expression → expression + term
expression → term
term → term * factor
term → factor
factor → id
factor → number
factor → ( expression )
if
statement has the
else
part?
if condition then
if condition then
statement
else
statement
O(N3) algorithm for parsing context-free
grammar, but particular subsets of CFG languages have "special
properties" which allow faster
(O(N))
algorithms (especially for parsing programming languages).
statement
you can decide whether which production to apply depending
on whether the next input symbol is
if,
for,
while,
or
identifer (expression statement)
Assignment 4 is about scheduling tasks when there is a dependency relationship among the tasks. The dependencies form a directed acyclic graph (DAG): a cycle in a dependency graph would mean that some task must be scheduled before and after some other task.
When a graph is a DAG, it expresses a partial order relationship. A topological sort is an enumeration of the vertices such that all the predecessor vertices of some vertex are listed before that vertex. There may not be a unique toplogical sort, but there will be at least one.
To perform a topological sort, we note that there must be at least one vertex with no incoming edges (otherwise, there would be a cycle). List all the vertices with no incoming edges (in any order) before all other edges. If those vertices are "removed" from the graph, the remaining smaller graph will still be a DAG and its root vertices can be listed next. Repeat until the last vertex is listed.
Given a topological sort of the task graph, the tasks can be easily scheduled because all predecessor tasks are scheduled before any dependent tasks (just schedule the task immediately after the last predecessor task completes).