
Presented By: Jason Bradbury
February 20, 1998
______________________________________________________________________________________
INTRODUCTION
______________________________________________________________________________
A client needs to access a timber sale across the Pilchcuck River. The proposed bridge construction must support a self propelled Washington 208 yarder and a Bendix Skagit T-90 Steel Tower with BU 737 drum yarder. The task of the FE Seniors is to design and provide preliminary assessments for
The following bridge analysis was performed using, the Forestry Handbook, PC Bridge program and the FERIC handbook.

Table 1 shows the front and rear axle loads for the Washington 208 and the BU-737 Yarders. The actual axle weights were unknown for both the yarders. Prof. Peter Schiess advised us to assume that 40% of the total vehicle weight was on the front axles of the Washington 208 Yarder. Since the BU-737 is similar to the Washington 108 (Table 7 from Austin Creek Bridge Project), and the front axle assumption is 30%, we used this assumption for the BU-737.
Log stringer Analysis using forestry handbook
Formulas used in determining stringer sizes for resistance to bending
2. Bh2 = 6M/f for rectangular timbers
Where
M = moment of dead log plus live load in inch-pounds
L = length of span, in feet
W = weight of floor and stringers in pounds per foot of span
b = width of stringer, in inches
h = depth of stringer, in inches
D = diameter of round timber, inside bark, at small end of log, in inches
S = spacing between stringers
f = extreme fiber stress in bending, in pounds per square inch
t = thickness of the bridge decking plus thickness of running surface
n = number of stringers
S = spacing of stringers center to center in feet
Bridge Calculations for Washington 208 Yarder using Douglas fir logs:
Calculation of weight per stringer (dead load):

Weight per stringer ![]()
Calculation of floor per stringer (dead load):
Number of stringers = 6
Width of roadway = 12.5 ft
Thickness of traverse decking = 3 inches
Thickness of run planks = 3 inches
Floor Weight per linear foot![]()
Calculation of Total Dead weight W:
W = Weight of floor + Weight of stringer
W = ![]()
Calculation of dead load bending moment ![]() :
:
L = length of free span = 40 ft
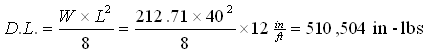
Calculation of Live Load Bending Moment ![]() :
:
Using vehicle Type D (Fig. 3, P. 18-37) with comparable gross vehicle weight of 175,000lbs. The Maximum Moment per Lane was estimated 800,000 ft-lbs. from the Forestry Handbook bridge graph (Fig. 17, pg. 18-39).
S = 28 inches center to center = 2.333 ft
![]()
Calculation of Total live and dead Load bending moments (M):
M = 2236800 in-lbs + 510504 in-lbs = 2,747,304 in-lbs
Calculation of minimum diameter needed for bridge (D):
f= extreme fiber stress in bending = 1450 psi (value found for Douglas Fir coastal region in Forestry handbook, Table 23, pg. 18-42)
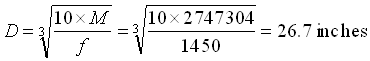
Therefore, the minimum small end diameter of each stringer is 27 inches.
This means that the tree must have a small end diameter of at least 27 inches to comply with the required mid-log diameter of 28 inches.
Bridge Calculations for Washington 208 Yarder using Glulam stringers:
Assumptions:
5 stringers
f = 1750 psi (Table 23.,p. 18-42)
b = 10.8 inches h = 39 inches bh2 = 16427 in3
Glulam weight = 50 ![]() (Table 16-3,pg. 16-11;USDA Timber Bridges Design, Construction, Inspection and Maintenance). Flooring weight = 40
(Table 16-3,pg. 16-11;USDA Timber Bridges Design, Construction, Inspection and Maintenance). Flooring weight = 40 ![]()
Calculation of weight per stringer (dead load):
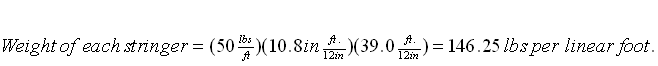
Calculation of floor per stringer (dead load):
Number of stringers = 5
Width of roadway = 12.5 ft
Thickness of traverse decking = 3 inches
Thickness of run planks = 3 inches
Floor Weight per stringer![]()
Calculation of Total Dead weight W:
W = Weight of floor + Weight of stringer
W = ![]()
Calculation of dead load bending moment ![]() :
:
L = length of free span = 40 ft
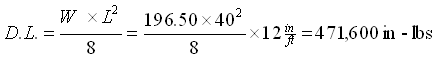
Calculation of Live Load Bending Moment ![]() :
:
Using vehicle Type D (Fig. 3, pg. 18-37) with comparable gross vehicle weight of 175,000 lbs. the Maximum Moment per Lane was estimated at 800,000 ft-lbs. from the Forestry Handbook bridge graph (Fig. 17, pg. 18-39). The moment on each stringer is taken as one-half of the total moment.
Therefore S = 37.5 inches center to center = 3.125 ft
Note: When the combined thickness of run planks and decking is 6 inches and the center to center spacing (S) is 4 feet or less, then S/5 is used. For 4-inch plank floors or 6-inch poles flattened to 4 inches S/4 is used.
![]()
Calculations of Total live and dead load bending moments (M):
M = 471,600 in-lbs + 3,000,000 in-lbs = 3,471,600 in-lbs
Minimum bh2 = (6M)/f
Calculation of minimum diameter needed for bridge (D):
f= extreme fiber stress in bending = 1750 psi (value found for Douglas Fir coastal region in Forestry handbook, Table 23, p 18-42)
bh2 = (6 * 3,471,600 in-lbs)/1750 psi) = 11,903 in3
The minimum bh2 = 11,903 cubic inches. This value is less than the above-calculated value of 16,427 cubic inches. Therefore the size and number of the glulam stringers is acceptable.
In Table 2, a number of different bridge configurations were analyzed for the Washington 208 and the Skagit BU-737 yarders. In the far right corner, the acceptable/overload rating is recorded. The Douglas fir logs with 28 inch diameter had a very close correlation between the needed and derived diameters. Even though most of the glulam designs were rated acceptable, we recommend the 8.8in by 39 in glulam stringer as the needed and derived bh2 values are very closely correlated. This is also the most cost efficient design, having the least number of stringers with the smallest dimensions.
TABLE 2. BRIDGE ANALYSIS
This table shows many different configurations of bridges and if they will support the listed vehicles.
|
Type |
Width (in.) |
Height (in.) |
# of Stringers |
Running Surface Width (ft) |
Length (ft) |
Vehicle |
Loaded GVW (lbs) |
Total Bending Moment (in-lb) |
D or bh2 Needed |
D or bh2 |
Rating |
|
Log |
28 inch diameter |
6 |
12.5 |
40 |
Washington 208 |
182,000 |
2747304 |
26.7 in. |
28 in. |
Acceptable |
|
|
Skagit BU 737 |
126,800 |
2271984 |
25.0 in. |
28 in. |
Acceptable |
||||||
|
Glulam |
10.9 |
46.5 |
4 |
12.5 |
40 |
Washington 208 |
182,000 |
3493500 |
11978 |
23352 |
Acceptable |
|
Skagit BU 737 |
126,800 |
2931000 |
10049 |
23352 |
Acceptable |
||||||
|
Glulam |
10.9 |
46.5 |
4 |
16 |
40 |
Washington 208 |
182,000 |
4354500 |
14930 |
23352 |
Acceptable |
|
Skagit BU 737 |
126,800 |
3634500 |
12461 |
23352 |
Acceptable |
||||||
|
Glulam |
10.9 |
46.5 |
4 |
12.5 |
60 |
Washington 208 |
182,000 |
7185375 |
24635 |
23352 |
Overload |
|
Skagit BU 737 |
126,800 |
5591625 |
19171 |
23352 |
Acceptable |
||||||
|
Glulam |
10.9 |
46.5 |
5 |
12.5 |
60 |
Washington 208 |
182,000 |
5936625 |
20354 |
23352 |
Acceptable |
|
Skagit BU 737 |
126,800 |
4661625 |
15983 |
23352 |
Acceptable |
||||||
|
Glulam |
8.9 |
39 |
4 |
12.5 |
40 |
Washington 208 |
182,000 |
3280920 |
11249 |
11405 |
Acceptable |
|
Skagit BU 737 |
126,800 |
2718420 |
9320 |
11405 |
Acceptable |
||||||
|
Glulam |
12.3 |
51 |
4 |
16 |
60 |
Washington 208 |
182,000 |
9168188 |
31434 |
31992 |
Acceptable |
|
Skagit BU 737 |
126,800 |
7128187 |
24440 |
31992 |
Acceptable |
||||||
|
Glulam |
8.9 |
39 |
3 |
12.5 |
40 |
Washington 208 |
182,000 |
4389250 |
15049 |
13537 |
Overload |
|
Skagit BU 737 |
126,800 |
3639250 |
12477 |
13537 |
Acceptable |
||||||
From figure 17, pg. 18-39, for a 40-foot span bridge, the maximum moment per lane for vehicle type D (175,000 lb. GVW) is 780,000 ft-lb. Since this
vehicle is slightly below our design vehicle of 182,000 lb, we used a maximum moment per lane of 800,000ft-lb.For BU-737, the alternate design vehicle, we used 630,000 ft-lb. as the maximum moment from figure 15, pg. 18-37 for type G (122,000 lb. GVW).
Log stringer Analysis using pc BRIDGE PROGRAM

Using the Bridge Program created by Jon Pascal and the equations found in the Forestry Handbook, pages 18-54 and 18-55, we were able to predict the truckload capability of the specified glulam bridge. Using the dimensions of the glulam stringer recommended in Table 2, the output program confirmed that the bridge was strong enough to withstand the vehicle loads of the Washington 208 and the Skagit BU-737 yarders.
In analyzing the log stringer bridge using Douglas-Fir, the value of f i.e. the extreme fiber in bending or tension parallel to grain was 1450 psi. For the glulam stringer design, the f value used was 1750 psi. This specific number was selected since it lies between the maximum and minimum values of f for Douglas-Fir, taken from Table 23, pg. 18-42 and should provide adequate strength for our proposed bridge.
In a stringer design example on pg. 106 of Weyerhaeuser glulam wood bridge systems, 1980, the f value used for Glulam stringers made of Douglas-Fir or southern pine (24f combination) was 2400 psi. These f value comparisons confirm that our glulam stringer is well within the acceptable limits.
log stringer Analysis using feric
Forest Engineering Research Institute of Canada (FERIC) Log Bridge Construction Handbook 1980 was used in determining the sizes of the mid stringers for the design truck load. Based on specifications determined by our client, we need to build a bridge with 28" mid-log diameter Douglas-fir stringers with a 40-foot maximum span length. The design is also based on a standard 3-inch running deck, rather than gravel. The vehicles considered are the Washington 208 yarder weighing 91 tons, and the Bendix Skagit T-90 Steel Tower with BU 737 drum yarder weighing 68 tons. Therefore, we assumed a 100-ton design truckload to accommodate either machine.
Table I-A on pg.11 of the FERIC Handbook shows the correlation between diameter sizes of mid stringers with maximum span length and design truckload. Since we have a 100-ton design truck load and 28" Douglas fir mid stringers, we need to use double-tier stringers for the bridge construction so as to get a maximum span length of 40 feet.
Double-tier stringers are positioned in tiers to enable many stringers to be fitted across the width of the bridge. For even load distribution, stringers should be grouped under the wheels of the vehicle. Figure 211 on pg. 261 shows the variation in spacing of stringer placement. Needlebeams are used to join the stringers and trussing system. For a span of 21-40 ft., four needlebeams are required.
Guardlogs are two stringers placed on the crossties directly above the outside stringers and tied to the crossties with a needlebeam. They must be the same size as the other stringers and must be pre-tensioned to carry their share of the dead load. In the event of extra clearance, steel needlebeams can be used. Figure 205 on pg. 257 shows a bridge cross-section with stringers as guardlogs. The guardlogs are fastened with wire rope saddles and slings. For our 100 ton design truckload, the cable size requirement for lashing is 7/8" for 100 ton design truck load. Figure 207 shows guardlogs lashed to a needlebeam with wire rope.
Douglas-fir green wood weighs 40 lbs/ft3. With a moisture content of 12%, it weighs 34 lbs/ft3. Logs and stringers are heavier owing to the large amount of sapwood in them. Therefore, an extra 2 to 3 lbs/ft3 should be added to the green weight on load calculations for logs and stringers.
If simple stringers are needed to build the log bridge then a 30" diameter Douglas-fir mid stringer should be used for 100 tons. Simple stringers might be a better construction design since they are less sensitive to overloading, decay, and damage. Stringers support the design load, and are therefore the most important and expensive part of the bridge design. However, they are also the most difficult bridge components to inspect and repair.
Recommendations using FERIC: Max. span length = 40 ft.; maximum truckload = 100 tons.
Reference: FERIC Stringer Designs by L.E. Gower (1980)