Chapter 8: Basic Plotting

Most of this information (and more) can be found in the Matlab help documentation in the section Basic Plotting Commands.

There are 6 stages of plotting data.

1. Prepare your data. If you don’ t think about how you are going to analyze your data when you are writing your experimental program then your analysis program will be a lot more complicated. One good idea is to create a fake data set and analyse it before collecting real data. This is often a good way of realizing that there may be issues in your experimental design that you hadn't thought of. It's also a great way of checking for bugs in your analysis code.

2. Decide which figures you want, and how you want them to be organized.

3. Plot the data

4. Set axis limits, tick marks etc.

5. Annotate the graph with x and y labels, titles and legends explaining each curve. Labels should be informative ("water-deprived" rather than "condition 1").

6. Print the figure, hold it out at arms’ length and see whether someone with presbyopia (your supervisor) will be able to read it.

99.8% of students omit stages 5-6. The easiest way to make your supervisor love you is to not forget those two stages.

Why use Matlab rather than Excel?

There are two reasons to plot data in Matlab rather than Excel.

1. Matlab is more powerful. Matlab makes it easy to explore data by plotting it in a wide variety of ways. This can help you get a greater insight into your data than you could by simply carrying out a standard set of tests. While you could easily use Excel to create all the plots that we create in this chapter, you will see examples of plotting data later in this book that would be very difficult or impossible in Excel.
2. It is easier to replot data using Matlab. You will find that you replot data repeatedly either as you collect more data, or as you (or your supervisor) think of new ways to look at it. A well written Matlab function will easily allow you to make modifications (e.g. throwing out outliers, only looking at male subjects) without having to entirely recreate the figure.

The figure window

Here we are simply closing any windows that might already be present, then putting up a figure window with no data in it so we can look at its properties.

close all

figure(1);

get(gcf);

Alphamap = [ (1 by 64) double array]

CloseRequestFcn = closereq

Color = [0.855388 0.855388 0.855388]

Colormap = [ (64 by 3) double array]

CurrentAxes = []

CurrentCharacter =

CurrentObject = []

CurrentPoint = [0 0]

DockControls = on

DoubleBuffer = on

FileName =

FixedColors = [ (3 by 3) double array]

IntegerHandle = on

InvertHardcopy = off

KeyPressFcn =

KeyReleaseFcn =

MenuBar = figure

MinColormap = [64]

Name =

NextPlot = add

NumberTitle = on

PaperUnits = inches

PaperOrientation = portrait

PaperPosition = [0.25 2.5 8 6]

PaperPositionMode = manual

PaperSize = [8.5 11]

PaperType = usletter

Pointer = arrow

PointerShapeCData = [ (16 by 16) double array]

PointerShapeHotSpot = [1 1]

Position = [-920 278 560 420]

Renderer = None

RendererMode = auto

Resize = on

ResizeFcn =

SelectionType = normal

ToolBar = auto

Units = pixels

WindowButtonDownFcn =

WindowButtonMotionFcn =

WindowButtonUpFcn =

WindowScrollWheelFcn =

WindowStyle = normal

WVisual = 00 (RGB 16 GDI, Bitmap, Window)

WVisualMode = auto

BeingDeleted = off

ButtonDownFcn =

Children = []

Clipping = on

CreateFcn =

DeleteFcn =

BusyAction = queue

HandleVisibility = on

HitTest = on

Interruptible = on

Parent = [0]

Selected = off

SelectionHighlight = on

Tag =

Type = figure

UIContextMenu = []

UserData = []

Visible = on

get(gcf) means "get me the properties of gcf". gcf is shorthand for "get current figure". So Matlab retrieves the current figure (the one that was most recently modified) and lists its properties. For people with experience with other programming languages, gcf is a handle (which is just another word for a pointer as far as most people are concerned) to the last figure that Matlab created. As you can see there are a lot of properties.

You can find out about, and change, the possible options for a property as follows. Suppose we want to find out how to change the the mouse pointer. We would find out what the possible alternatives are as follows.

set(gcf, 'Pointer')

[ crosshair | fullcrosshair | {arrow} | ibeam | watch | topl | topr | botl | botr | left | top | right | bottom | circle | cross | fleur | custom | hand ]

And to change the properties of the mouse pointer we specify what sort of pointer we want.

set(gcf, 'Pointer', 'fleur')

You can also change various other figure properties using the set command.

set(gcf, 'Color', [1 1 .5])

set(gcf, 'Position', [100 100 300 300])

set(gcf, 'PaperOrientation', 'landscape');

set(gcf, 'Name', 'My Data Figure');

Sometimes you will have more than one figure and want to be able to access and change properties on one that isn't the most recent figure. In that case you need to create a handle to each figure.

close all

f1=figure(1);

f2=figure(2);

set(f1, 'Color', [1 1 .5]);

set(f2, 'Color',[0 1 1]);

You can also put figure handles into an array as if they were a list of numbers.

clear all

close all

clist=[1 1 .5; .5 1 1];

for i=1:2;

f(i)=figure(i);

set(f(i), 'Color', clist(i, :));

end

Axes

Any data plot is contained within an axis. A figure by default will contain a single axis, but it's possible to create a set of subplots (axes) within a single figure window. This code creates a figure window organized so as to contain two rows and two columns of subplots, and calls up the first of those subplots.

close all

figure(1)

subplot(2,2,1)

Here's another example.

close all

figure(1)

subplot(2, 1, 2)

Like figures, subplots have various properties which are accessed in a very similar way that as figure properties. Here gca stands for get current axis, and allows you to get the properties of the most recently modified subplot.

get(gca)

ActivePositionProperty = position

ALim = [0 1]

ALimMode = auto

AmbientLightColor = [1 1 1]

Box = off

CameraPosition = [0.5 0.5 9.16025]

CameraPositionMode = auto

CameraTarget = [0.5 0.5 0.5]

CameraTargetMode = auto

CameraUpVector = [0 1 0]

CameraUpVectorMode = auto

CameraViewAngle = [6.60861]

CameraViewAngleMode = auto

CLim = [0 1]

CLimMode = auto

Color = [1 1 1]

CurrentPoint = [ (2 by 3) double array]

ColorOrder = [ (7 by 3) double array]

DataAspectRatio = [1 1 1]

DataAspectRatioMode = auto

DrawMode = normal

FontAngle = normal

FontName = Helvetica

FontSize = [10]

FontUnits = points

FontWeight = normal

GridLineStyle = :

Layer = bottom

LineStyleOrder = -

LineWidth = [0.5]

MinorGridLineStyle = :

NextPlot = replace

OuterPosition = [0 0.0654626 1 0.404885]

PlotBoxAspectRatio = [1 1 1]

PlotBoxAspectRatioMode = auto

Projection = orthographic

Position = [0.13 0.11 0.775 0.341163]

TickLength = [0.01 0.025]

TickDir = in

TickDirMode = auto

TightInset = [0.0392857 0.0404762 0.00892857 0.0190476]

Title = [162.003]

Units = normalized

View = [0 90]

XColor = [0 0 0]

XDir = normal

XGrid = off

XLabel = [159.003]

XAxisLocation = bottom

XLim = [0 1]

XLimMode = auto

XMinorGrid = off

XMinorTick = off

XScale = linear

XTick = [ (1 by 11) double array]

XTickLabel = [ (11 by 3) char array]

XTickLabelMode = auto

XTickMode = auto

YColor = [0 0 0]

YDir = normal

YGrid = off

YLabel = [160.003]

YAxisLocation = left

YLim = [0 1]

YLimMode = auto

YMinorGrid = off

YMinorTick = off

YScale = linear

YTick = [ (1 by 6) double array]

YTickLabel =

0

0.2

0.4

0.6

0.8

1

YTickLabelMode = auto

YTickMode = auto

ZColor = [0 0 0]

ZDir = normal

ZGrid = off

ZLabel = [161.003]

ZLim = [0 1]

ZLimMode = auto

ZMinorGrid = off

ZMinorTick = off

ZScale = linear

ZTick = [0 0.5 1]

ZTickLabel =

ZTickLabelMode = auto

ZTickMode = auto

BeingDeleted = off

ButtonDownFcn =

Children = []

Clipping = on

CreateFcn =

DeleteFcn =

BusyAction = queue

HandleVisibility = on

HitTest = on

Interruptible = on

Parent = [1]

Selected = off

SelectionHighlight = on

Tag =

Type = axes

UIContextMenu = []

UserData = []

Visible = on

Note that an axis has different properties from those of a figure. Once again you can look at the various options you have for axis properties using set.

set(gca, 'FontWeight')

[ light | {normal} | demi | bold ]

Here’s a list of the most useful properties of axes that you might want to change. As you go through these commands look at how the figure changes. But you can also find and modify lots of other properties using get(gca) and set(gca).

clear all

close all

figure(1)

set(gcf, 'Color', [.2 .7 1]);

a1=subplot(1, 2, 1);

a2=subplot(1, 2, 2);

axis color properties

set(a1, 'Color', [1 1 .7]); % Sets the color inside the subplot.

set(a2, 'Color', [.7 1 1]);

axis font properties

set(a1, 'FontName', 'Times');

set(a1, 'FontSize', 12);

set(a1, 'FontWeight', 'bold')

set(a2, 'FontName', 'Arial');

set(a2, 'FontSize', 16);

axis labelling

Note that you need to use a slight variant of terminology for title and axis labelling.

title(a1, 'Ugly Plot 1');

XLabel(a1, 'my x axis');

YLabel(a1,'my y axis');

title(a2, 'Ugly Plot 2');

XLabel(a2,'your x axis');

YLabel(a2,'your y axis');

Warning: Could not find an exact (case-sensitive) match for 'XLabel'.

C:\Program Files\MATLAB\R2007b\toolbox\matlab\graph2d\xlabel.m is a

case-insensitive match and will be used instead.

You can improve the performance of your code by using exact

name matches and we therefore recommend that you update your

usage accordingly. Alternatively, you can disable this warning using

warning('off','MATLAB:dispatcher:InexactMatch').

Warning: Could not find an exact (case-sensitive) match for 'YLabel'.

C:\Program Files\MATLAB\R2007b\toolbox\matlab\graph2d\ylabel.m is a

case-insensitive match and will be used instead.

You can improve the performance of your code by using exact

name matches and we therefore recommend that you update your

usage accordingly. Alternatively, you can disable this warning using

warning('off','MATLAB:dispatcher:InexactMatch').

axis limits, tick placement and tick labelling

Note how you can use either text or a vector to replace default tick labels with whatever you want. Here we are using a cell array to label our axes.

set(a1, 'XLim', [0 .5]);

set(a2, 'XLim', [0 3]);

set(a2, 'YLim', [1 1000]);

set(a2, 'XTick', 0:1:3);

set(a2, 'YTick', [1 100 1000]);

set(gca,'XTickLabel',{'Zero';'One';'Two';'Three'})

set(gca, 'YTickLabel', [1 1/100 1/1000]);

Other useful commands

axis(a1, 'equal'); % Sets the axis so tick marks are equally spaced on x and y axes

axis(a1, 'square') % makes the current axis square

axis(a1,'off')% turns off all axis labeling, tick marks etc.

Plotting

Now we are going to plot data on the axes. Once again, plots have properties that you can alter. The kinds of properties you can change depend on the kind of plot you are making.

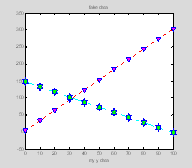
Let's start with a line plot. The command hold tells Matlab to include both plots in the figure rather than simply overwriting the first plot with the second.

clear all

close all

figure(1)

x=0:10:100;

y1=3*x+4;

y2=150-(y1/2);

p1=plot(x, y1);

hold on

p2=plot(x, y2);

Color

First we'll define the color of these plots. One way to do this is to specify the level of the red, green or blue guns, using values between 0-1.

set(p1, 'Color', [ 1 0 0]);

Alternatively you can use shorthand for some specific colors. Options include: 'b', 'g', 'r', 'c', 'm', 'y', 'k' (blue, green, red, cyan, magenta, yellow black).

set(p2, 'Color', 'c');

Line style and markers

set(p1, 'LineWidth', 1)

set(p1, 'LineStyle', ':');

set(p2, 'LineWidth', 2)

set(p2, 'LineStyle', '-.');

Options include: '-', '-– ', ':', '-.', 'none' (solid line, dashed line, dotted line, dash-dot line, no line)

set(p1, 'MarkerSize', 10);

set(p1,'MarkerEdgeColor' , [0 0 1])

set(p1, 'MarkerFaceColor', [1 0 1])

set(p1, 'Marker', 'v');

set(p2, 'MarkerSize', 15);

set(p2,'MarkerEdgeColor' , [0 0 1])

set(p2, 'MarkerFaceColor', [0 1 0])

set(p2, 'Marker', 'h');

Options for Marker include '+', 'o ', '* ', '.', 'x', 's', 'd', '|', 'v ', '^', '> ', '<' ,'p', 'h', 'none'. The 'v', '<', '>', '^' symbols represent triangles of various orientations

Legends and Text

Legends and text are manipulated using handles in a very similar way to plots. Because we only have a single plot in our figure window we don't need to specify which axis we are labelling.

title('fake data');

xlabel('my x data');

xlabel('my y data');

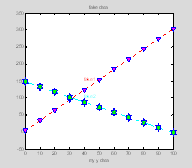
text

text takes as input the x and y position of the string you want to position, and the text string itself. These text objects can also be assigned handles and you can change their properties. To manipulate properties you once again use get and set.

t1=text(x(5), y1(6), 'fake 1');

t2=text(x(5), y2(4), 'fake 2');

set(t1,'Color', 'r');

set(t2,'Color', 'c');

get(t1)

Annotation = [ (1 by 1) hg.Annotation array]

BackgroundColor = none

Color = [1 0 0]

DisplayName =

EdgeColor = none

EraseMode = normal

Editing = off

Extent = [39.5402 142.42 8.50575 20.9913]

FontAngle = normal

FontName = Helvetica

FontSize = [10]

FontUnits = points

FontWeight = normal

HorizontalAlignment = left

LineStyle = -

LineWidth = [0.5]

Margin = [2]

Position = [40 154 0]

Rotation = [0]

String = fake 1

Units = data

Interpreter = tex

VerticalAlignment = middle

BeingDeleted = off

ButtonDownFcn =

Children = []

Clipping = off

CreateFcn =

DeleteFcn =

BusyAction = queue

HandleVisibility = on

HitTest = on

Interruptible = on

Parent = [158.003]

Selected = off

SelectionHighlight = on

Tag =

Type = text

UIContextMenu = []

UserData = []

Visible = on

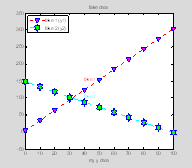
legend

legend takes in a list of the plot handles for which you want to create legend entries, and a list of the strings that will be the legend labels (again, don't worry about the squiggly brackets, we'll get to them soon)

ActivePositionProperty: 'position'

ALim: [0 1]

ALimMode: 'auto'

AmbientLightColor: [1 1 1]

Box: 'on'

CameraPosition: [0.5000 0.5000 17.3205]

CameraPositionMode: 'auto'

CameraTarget: [0.5000 0.5000 0]

CameraTargetMode: 'auto'

CameraUpVector: [0 1 0]

CameraUpVectorMode: 'auto'

CameraViewAngle: 6.6086

CameraViewAngleMode: 'auto'

CLim: [0 1]

CLimMode: 'manual'

Color: [1 1 1]

CurrentPoint: [2x3 double]

ColorOrder: [7x3 double]

DataAspectRatio: [1 1 2]

DataAspectRatioMode: 'auto'

DrawMode: 'fast'

FontAngle: 'normal'

FontName: 'Arial'

FontSize: 10

FontUnits: 'points'

FontWeight: 'normal'

GridLineStyle: ':'

Layer: 'bottom'

LineStyleOrder: '-'

LineWidth: 0.5000

MinorGridLineStyle: ':'

NextPlot: 'add'

OuterPosition: [0.1351 0.8032 0.2232 0.1048]

PlotBoxAspectRatio: [1 1 1]

PlotBoxAspectRatioMode: 'auto'

Projection: 'orthographic'

Position: [0.1423 0.8079 0.2125 0.1000]

TickLength: [0.0100 0.0250]

TickDir: 'in'

TickDirMode: 'auto'

TightInset: [0.0071 0.0048 0.0036 0]

Title: 215.0032

Units: 'normalized'

View: [0 90]

XColor: [0 0 0]

XDir: 'normal'

XGrid: 'off'

XLabel: 216.0032

XAxisLocation: 'bottom'

XLim: [0 1]

XLimMode: 'manual'

XMinorGrid: 'off'

XMinorTick: 'off'

XScale: 'linear'

XTick: -1

XTickLabel: ''

XTickLabelMode: 'manual'

XTickMode: 'manual'

YColor: [0 0 0]

YDir: 'normal'

YGrid: 'off'

YLabel: 217.0032

YAxisLocation: 'left'

YLim: [0 1]

YLimMode: 'manual'

YMinorGrid: 'off'

YMinorTick: 'off'

YScale: 'linear'

YTick: -1

YTickLabel: ''

YTickLabelMode: 'manual'

YTickMode: 'manual'

ZColor: [0 0 0]

ZDir: 'normal'

ZGrid: 'off'

ZLabel: 218.0032

ZLim: [-1 1]

ZLimMode: 'auto'

ZMinorGrid: 'off'

ZMinorTick: 'off'

ZScale: 'linear'

ZTick: [-1 0 1]

ZTickLabel: ''

ZTickLabelMode: 'auto'

ZTickMode: 'auto'

BeingDeleted: 'off'

ButtonDownFcn: {2x1 cell}

Clipping: 'on'

CreateFcn: []

DeleteFcn: []

BusyAction: 'queue'

HandleVisibility: 'on'

HitTest: 'on'

Interruptible: 'off'

Selected: 'off'

SelectionHighlight: 'on'

Tag: 'legend'

Type: 'axes'

UIContextMenu: 176.0032

UserData: [1x1 struct]

Children: [6x1 double]

Parent: 1

Visible: 'on'

Location: 'NorthWest'

Orientation: 'vertical'

EdgeColor: [0 0 0]

TextColor: [0 0 0]

Interpreter: 'tex'

String: {'fake 1 (y1)' 'fake 2 (y2)'}

lh=legend([p1 p2], {'fake 1 (y1)'; 'fake 2 (y2)'}, 'Location', 'NorthWest');

set(lh, 'FontName', 'Arial', 'FontSize', 10);

get(lh)

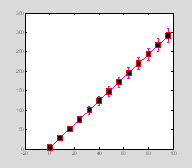
Errorbar plots

close all

x=0:8:100;

y=3*x+4;

err=sqrt(y);

ph=errorbar(x, y, err);

set(ph, 'Marker', 's', 'MarkerSize', 13, ...

'MarkerFaceColor', 'k', 'MarkerEdgeColor', 'r', 'Color', 'm', 'LineWidth', 2)

One inconvenient thing about the errorbar plots automatically generated by Matlab is that the errorbar always have same properties (e.g. color and line thickness) as the main line. Sometimes you want the error bars to have different properties. The way to do this is to draw the main line and the error bar as overlapping plots, i.e. use the error bars as an overlay. Here we start by creating a plot with black dotted lines and triangular symbols. Notice how we use a single set command to define multiple properties.

close all

x=0:8:100;

y=300-3*x+4;

err=sqrt(2*x);

p=plot(x, y);

set(p, 'Color', 'k', 'LineStyle', ':', 'LineWidth', 2, 'Marker', 'v', 'MarkerSize', 10,'MarkerEdgeColor' , 'k', 'MarkerFaceColor','k');

Then we add gray error bars. We define this plot as having no line and no marker so only the actual error bars are visible.

hold on

e=errorbar(x, y, err);

set(e, 'Color', [.5 .5 .5], 'LineStyle', 'none', 'LineWidth', 1, 'Marker', 'none');

Log plots

clear all

close all

figure(1)

x=0.1:.1:4.5;

y=exp(x);

subplot(1, 3, 1);

plot(x, y, '.-', 'MarkerSize', 10, 'Color', 'k');

set(gca, 'YLim', [0 100]);

title('linear plot');

subplot(1, 3, 2)

semilogy(x, y, '.-', 'MarkerSize', 10, 'Color', 'k');

title('log y plot');

set(gca,'YLim',[0 100]);

subplot(1, 3, 3)

loglog(x, y, '.-', 'MarkerSize', 5, 'Color', 'k');

title('log log plot');

%set(gca, 'YLim', [0 100]);

As is shown in the second and third subplots, it is possible to plot logarithmic data along either the x axis (semilogx), the y axis (semilogy), or both axes (loglog).

You may find it a little annoying that the y-axis labels are expressed in base 10. There’s no way of changing that using the matlab semilogx and semilogy commands, but there is a workaround which is explained in Section 3 (see logx2raw, logy2raw).

Bar plots

Here's how to create a simple bar plot, and change some basic properties using handles.

close all

x=0:5:20;

y=[3*x+4];

ph=bar(x, y);

Bar properties

set(ph, 'BarWidth', .5);

set(ph, 'EdgeColor', 'r')

set(ph, 'LineWidth', 1.5);

set(ph, 'FaceColor',[0 1 1 ]);

More complex bar plots

With bar plots using more than one set of y-values you will get a handle for each set of data (similarly to plotting line data using plot). Here we have two sets of y data for every x-value

clear all; close all

x=0:5:20;

y=[3*x+4;2*x+2]';

bh=bar(x, y);

set(bh(1), 'FaceColor',[1 0 1 ])

set(bh(2), 'FaceColor',[0 .3 1 ])

set(gca, 'XTickLabel',...

{'Day 1', 'Day 5', 'Day 10', 'Day 15','Day 20'})

legend([bh(1) bh(2)], 'Happy', 'Sad', 'Location', 'NorthWest')

Bar plots with error bars

Matlab doesn’t have a function to do this, so you need to use a work around. You add errorbars to bar plots in a vaery similar way as plotting them as an overlay to line plots. You may have to fiddle with the parameter width to make it look right.

hold on

width=get(bh(1), 'BarWidth')-.1;

eh1=errorbar(x-width, y(:, 1), y(:, 1)/4, ...

'Marker', 'none','Color', 'k', 'LineStyle', 'none');

eh2=errorbar(x+width, y(:, 2), y(:, 2)/5, ...

'Marker', 'none','Color', 'k', 'LineStyle', 'none');

Note that this is the sort of thing that makes a very good function.

Histograms

clear all; close all

data=randn(3000, 1);

hist(data, 9);

set(gca, 'XLim', [-4.5 4.5])

Here you have asked for your data to be divided into 9 bins. If you want to know what the center of the bins are you can ask hist to return the number of data points in each bin (n1) and the centers of the bins (x1) instead of plotting the data. If you want to then plot the histogram then you will need to call hist twice.

[n1, x1]=hist(data, 5);

figure(1); clf; hist(data, 5);

n1

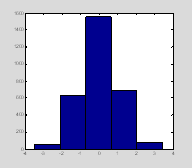x1

n1 =

53 627 1556 692 72

x1 =

-2.8111 -1.4280 -0.0450 1.3381 2.7212

You can also give hist a vector of the bin centers. Here we only collect the return argument that tells us the number of data points that fell within each bin. We already know where the bin centers are, because we defined them. We can then plot the histogram using bar.

bins=-4:.25:4;

subplot(1, 3,2);

n1=hist(data, bins);

figure(1); clf;

hist(data, bins)

clf clears all plots in the current figure window without closing the actual window. Sometimes you have your command window and your figure windows nicely arranged on the screen so you can see them all at once. clf leaves the figure window up, so you don't have to keep repositioning it every time you replot data.

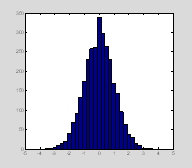histc takes in a vector that contains the upper and lower limits of each bin. It returns the number of data points that fell within each bin. Note that the bins are no longer equally spaced.

bins=[-5, -3:1:3, 5];

n2=histc(data, bins);

figure(1); clf;

histc(data, bins);

Other useful 2d plot commands

Use doc (e.g. doc polar) to learn about these commands. plotyy

polar

stairs

stem

An example of plotting

Let's imagine you've collected data measuring students' reaction times to moving stimuli and their reading speed. You've done this for both males and females, and you've recorded whether the subjects play video games vs. non-gamers. You have the following subject break down:

10 males, 10 females

6 of the 10 males are gamers

4 of the 10 females are gamers.

In this program, GamersAnon.m, we'll begin by faking our data, and then we'll plot it as both a bar graph and a scatter plot.

% GamersAnon.m

%

% A fake experiment examining the effects of gaming on reading speed

% and motion RTs

clear all

% fake data

data=zeros(4, 20);

data(1, 1:10)=1; % 0 = male, 1 = female

data(2, [[1:6], [11:14]])=1; % 0 = non-gamer, 1=gamer

data(3, :)=180; % default RT speed is 180ms

data(3, [[1:6], [11:14]])=data(3, [[1:6], [11:14]])-30;

% gamers are 30ms faster

data(3, :)=round(data(3, :)+8*randn(size(data(3, :)))); % add random noise

data(4, :)=50; % default wpm

data(4, [[1:6], [11:14]])=40; % gamers are slower

data(4, :)=round(data(4, :)+ 4*randn(size(data(4, :)))); % add random noise

So your data looks like this:

data

data =

Columns 1 through 12

1 1 1 1 1 1 1 1 1 1 0 0

1 1 1 1 1 1 0 0 0 0 1 1

157 149 146 150 139 148 165 192 176 186 166 143

43 39 45 40 38 39 56 50 49 52 40 41

Columns 13 through 20

0 0 0 0 0 0 0 0

1 1 0 0 0 0 0 0

147 145 178 188 165 189 186 181

39 42 55 48 53 48 49 50

Now let's plot the data in a bar graph

gender={'male', 'female'};

gamer={ 'non-gamer', 'gamer'};

task = { 'motion', 'reading'};

%% bar graph

figure(1); clf;

for k=1:2 % task

for i=1:2 % male / female

for j=1:2 % gamer / non-gamer

ind= find(data(1, :)==i-1 & data(2, :)==j-1);

tmp=data(2+k,ind);

MeanData(k, i, j)= mean(tmp);

StdData(k, i, j)= std(tmp);

SemData(k, i, j)=std(tmp)/sqrt(length(tmp));

end

end

subplot(2, 1,k)

b1=bar(squeeze(MeanData(k, :, :))); hold on

title(task{k});

set(gca, 'XTickLabel', gender);

if k==1

YLabel('RT (ms)');

else

YLabel('Reading speed (wpm)');

h=legend(gamer);

set(h, 'Location', 'SouthEast');

end

end

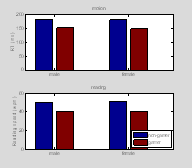We use these nested for loops and find to extract the data for each condition. When setting up these loops you need to think carefully about how you want your figures to be organized. We have a couple of other examples of how to do this later in this chapter.

squeeze is a funny command. Let's say you have a 3D matrix, but you only want two dimensions from it (a slice from the cube). If you take the slice along anything but the last dimension then Matlab still considers this 2D slice as being 3D – it's a 3D matrix of size 1 x n x m. squeeze "squeezes" this 3D slice into an m x n 2D matrix.

Notice in the example below that b and c are identical in their contents, but Matlab thinks that b has a size of 1 x 2 x 3 whereas c is simply a 2 x 3 matrix.

a=randn(2, 2, 3);

b=a(1, :, : )

size(b)

b(:,:,1) =

-0.2709 -1.4115

b(:,:,2) =

0.5554 -1.2399

b(:,:,3) =

0.7854 1.1957

ans =

1 2 3

c=squeeze(b)

size(c)

c =

-0.2709 0.5554 0.7854

-1.4115 -1.2399 1.1957

ans =

2 3

Now let's look at our data in a scatter plot.

colorlist=[0 0 1; 1 0 1];

symlist=['s', 'o'];

figure(2); clf;

for i=1:2 % male / female

for j=1:2 % gamer / non-gamer

ind=find(data(1, :)==i-1 & data(2, :)==j-1);

tmp1=data(3,ind);

tmp2=data(4,ind);

plot(tmp1, tmp2, '.', 'MarkerSize', 6, 'Color', colorlist(i ,:), 'Marker', symlist(j), 'MarkerFaceColor', [1 1 1]);

hold on

% overlay larger solid color symbols for the mean response

% for male gamers, female gamers, etc. etc.

h(i, j)=plot(MeanData(1, i, j), MeanData(2, i, j), 'MarkerSize', 12, 'Color', colorlist(i ,:),'Marker', symlist(j), 'MarkerFaceColor', colorlist(i ,:));

end

end

XLabel('RT (ms)');

YLabel('Reading speed (wpm)');

legend(h(:), 'M gamer', 'D gamer','M non-gamer', 'F non-gamer','Location', 'SouthEast');

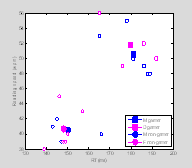Plotting in 3d using mesh

Suppose you were looking at how age affects your ability to perform a task as a function of the time of day. So in this example, Sleepyhead.m, you have two independent variables, the time of day and the age of the subject, and one dependent variable, which is performance. Your data might look like this:

% Sleepyhead

%

% An example of using mesh to view 3D data with 2 independent and one dependent variable

clear all

age=[17 17.5 18 18.5 19 19 40 45 47 50 60 65 67 68 69 70];

tod=[9 11 1 3 5 7 9];

tod(3:end)=tod(3:end)+12; % move to the 24 hour clock!

perf=[90 90 80 80 85 80 80 ;

90 80 80 80 90 90 95 ;

90 90 90 80 90 85 90 ;

80 90 75 70 80 90 85 ;

80 80 80 70 80 100 90 ;

85 80 90 75 90 85 85 ;

90 85 80 70 80 67 40 ;

100 80 80 70 80 58 30 ;

80 75 70 65 75 60 36 ;

80 80 70 80 70 60 40 ;

90 90 90 80 50 40 20 ;

90 90 90 70 80 40 30 ;

85 90 87 70 80 35 22 ;

80 85 80 75 65 45 22 ;

95 83 85 85 75 38 25 ;

90 80 90 80 80 36 18];

We are going to plot our data using mesh(x,y,Z). The rule for mesh is that first two vectors must have length(x) = n and length(y) = m where [m,n] = size(Z).

figure(1); clf;

sh=mesh(tod, age, perf);

xlabel('time of day');

ylabel('Age (years)');

zlabel('Performance');

You can now play with various aspects of the figure

shading flat

shading interp

colormap(gray)

One useful command is view. You can rotate your view of this three-D graph manually using the mouse if you hit the little rotation icon on the top of the menu bar. If you rotate the graph to a good view, you might then want to save the values that represent that view so you don’t have to manipulate it by hand the next time you plot the data. view allows you to save that viewpoint.

v=view;

You can then set the view to the desired view which you previously saved by using a viewmatrix as an input argument.

view(v);

Try saving a viewpoint, then rotate the graph manually, and use view to restore the graph to the saved viewpoint.

Alternatively you can provide view with the azimuth and elevation you desire (the azimuth and elevation are basically simpler forms of the 4x4 matrix contained in v)

view(60, 50)

There are also three default views.

view

view(2);

view(3);

ans =

0.5000 0.8660 0 -0.6830

-0.6634 0.3830 0.6428 -0.1812

-0.5567 0.3214 -0.7660 9.1609

0 0 0 1.0000

Also try:

surf(tod, age, perf);

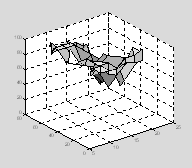
Surf and mesh can deal with missing data values as long as they are set to be NaN (not a number). Surf and mesh will simply interpolate between the missing values.

perf(3,1)=NaN;

perf(5,3)=NaN;

perf(7,2)=NaN;

sh=surf(tod, age, perf);

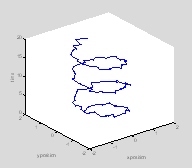
Plot3

This is often useful when you have one independent and two dependent variables. One example would be if you were tracking the x and y position of a rat over time, as in this example Ratty.m.

% Ratty.m

%

% tracks the x and y position of a rat moving in space over time.

clear all

figure(1); clf;

t = linspace(0,6*pi,101);

% fake the data

x = sin(t)+.1*randn(size(t));

y = cos(t)+.1*randn(size(t));

% plot x & y position over time

plot3(x, y, t, '.-');

xlabel('x position');

ylabel('y position');

zlabel('time')

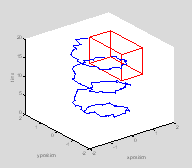
This rat is a little confused. Let’s suppose you were interested in seeing whether the rat reached a certain location (food or a swim platform) within a certain space-time window. First let’s plot the position of this target on the graph.

twin=[10 17]; % target time is 10-17 seconds

xwin=[0.7 1.7]; % target platform lies between these x co-ordinates

ywin=[-.5 1.5]; % target platform lies between these y co-ordinates

edgeoftarget=[1 2 1 1 1 1; ...

1 2 1 1 2 2; ...

1 2 2 2 1 1 ; ...

1 2 2 2 2 2; ...

1 1 1 2 1 1; ...

1 1 1 2 2 2; ...

2 2 1 2 1 1 ; ...

2 2 1 2 2 2; ...

1 1 1 1 1 2; ...

1 1 2 2 1 2; ...

2 2 1 1 1 2; ...

2 2 2 2 1 2];

for i=1:size(edgeoftarget, 1)

lh=line([xwin(edgeoftarget(i, 1)) xwin(edgeoftarget(i, 2))], ...

[ywin(edgeoftarget(i, 3)) ywin(edgeoftarget(i, 4))], ...

[twin(edgeoftarget(i, 5)) twin(edgeoftarget(i, 6))]);

set(lh, 'Color', 'r');

end

ind=find(t>=twin(1) & t<twin(2) & x>=xwin(1) & x<xwin(2) & ...

y>=ywin(1) & y<ywin(2));

hold on

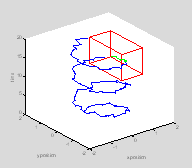
Now re-plot those points in the rat's history when she is inside the target box in green

plot3(x(ind), y(ind), t(ind), 'g.-');

Saving figures

It's possible to save figures in a variety of formats. Here we'll save the rat pathway as a tif figure.

saveas(gcf, 'RattyPathway', 'tif');

disp(['figure saved in directory ', pwd])

figure saved in directory C:\Program Files\MATLAB\R2007b