I'm confused about how the vectors for problem 78 in chapter 4 are setup. The wording in the question makes it extremely hard to discern what the relationship between the air/ground velocity/direction of the plane are. Could you possibly post a picture of the vectors?
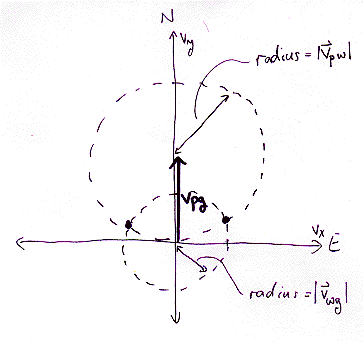
Well, sort of... the point of the problem is that the exact geometry of the vectors needs to be determined. What you know is that the vector equation v_wg + v_pw = v_pg holds, and that the vector v_pg = 150mi/h yhat. In the graph below, the dashed circle centered about the origin has a radius equal to the magnitude of v_wg, and the circle centered about the head of v_pg has a radius of v_pw. So, due to the constraints imposed by the magnitudes of the vectors v_pw and v_wg, a final picture of the vectors will have v_wg starting at the origin and ending at one of the intersection dots, and then have v_pw starting at the chosen intersection point and ending at the head of v_pg. You should be able to use either analytic geometry or the law of cosines to answer the problem.
