SMARTPsych SPSS Tutorial

Between-Subjects Analysis of Variance

 

 

Step 1:  Enter your data.

 

Text Box: Begin by entering your data in the same manner as for an independent groups t-test. You should have two columns: 1) the dependent variable 2) a grouping variable

 

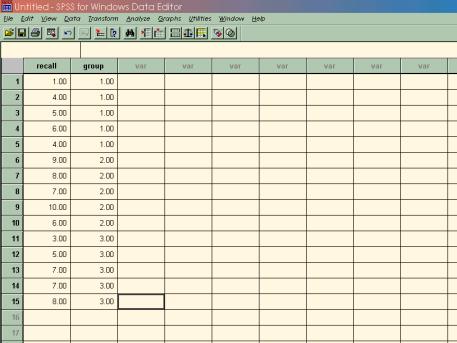
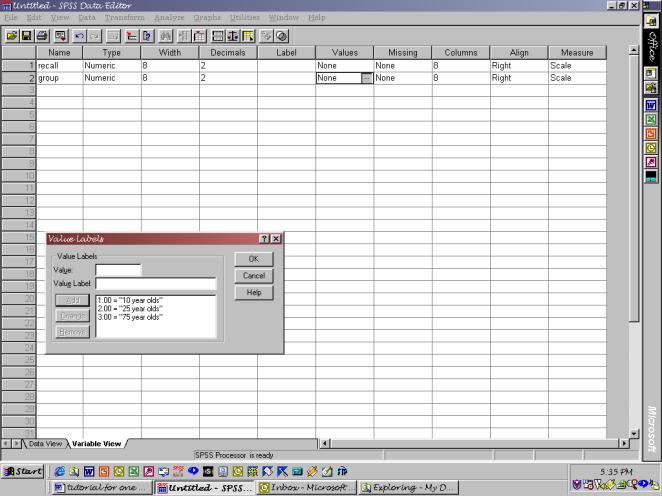
Step 2:  Define your variables.

 

Remember that to do this, you can simply double-click at the top of the variable’s column, and the screen will change from “data view” to “variable view,” prompting you to enter properties of the variable.  For your dependent variable, giving the variable a name and a label is sufficient.  For your independent variable (the grouping variable), you will also want to have value labels identifying what numbers correspond with which groups.  See the following figure for how to do this.


Step 3: Select Oneway ANOVA from the command list in the menu as follows:

 


 

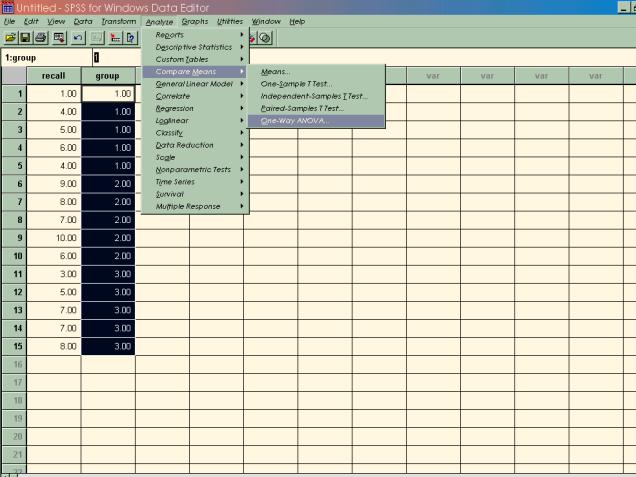
Note:  There is more than one way to run this command in SPSS.  For now, the easiest way to do it is to go through the “compare means” option.   However, since the analysis of variance procedure is based on the general linear model, you could also use the analyze/general linear model option to run the ANOVA.  This command allows for the analysis of much, much more sophisticated experimental designs than the one we have here, but using it on these data would yield the same result as the One-way ANOVA command.

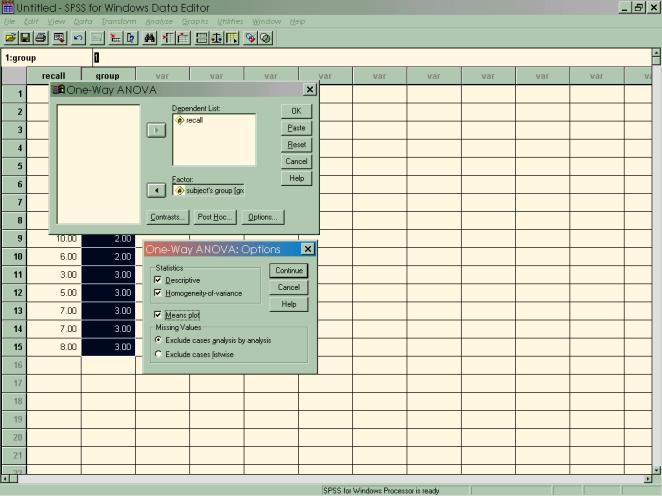
Step 4: Run your analysis in SPSS.

Once you’ve selected the One-way ANOVA, you will get a dialog box like the one at the top.  Select your dependent and grouping variables (notice that unlike in the independent samples t-test, you do not need to define your groups—SPSS assumes that you will include all groups in the analysis.

 

Text Box: While you’re here, you might as well select the “options…” button, and check that you would like descriptive and HOV statistics. You can also select for SPSS to plot the means if you like.


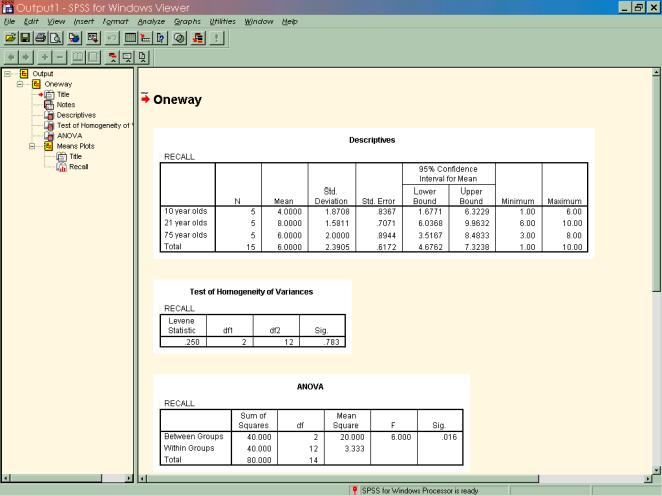
Step 5: View and interpret your output.

 

Text Box: WOW! Look at all this information! Note that the descriptive statistics include CIs, your HOV test is in a separate table from your descriptive statistics, and your ANOVA partitions your sum of squares.

 

But some of you are begging to know, how can I do all of this with syntax commands?  You can see what the syntax looks like by selecting “paste” when you are in the One-way ANOVA dialog box.

Step 6: Now that you know how to run a between-subjects ANOVA, enter the data from the following problem and run through the previous steps on your own.

 

In a verbal learning task, nonsense syllables are presented for later recall.  Three different groups of subjects see the nonsense syllables at a 1-, 5-, or 10-second presentation rate.  The data (number of errors) for the three groups are as follows:

 

            1-second group                        5-second group                        10-second group

                        13                                            11                                            3

                        15                                            14                                            5

                        15                                            13                                            6

                        12                                            12                                            6

                        13                                            16                                            9

                        12                                            12                                            7

                        9                                              11                                            2

                        8                                              9                                              4

15                                                                                       10                                            3

12                                            8                                              1

8                                              9                                              8

 

a.)    Do a boxplot to see what the distributions look like.

b.)   Perform an ANOVA on the data.