Beginning Scientific Computing

Video Lectures and Supplementary Tutorials

LOADING
  • Stacks Image 1151

    Advanced Numerical Algorithms through MATLAB

  • Stacks Image 1153

    Three-body Problem of Celestial Mechanics and Chaotic Behavior

  • Stacks Image 1155

    Programming in MATLAB

  • Stacks Image 1262

    Gradient Descent for Optimization

  • Stacks Image 1264

    Fourier Transform and Applications

  • Stacks Image 1266

    Quadrature Rules for Integration

  • Stacks Image 1268

    Newton-Raphson Iteration Methods

  • Stacks Image 1270

    Principal Component Analysis from SVD

About This Course

 

This webpage is designed to provide a easy access point for all video materials related to AMATH 301: Beginning Scientific Computing (Department of Applied Mathematics, University of Washington). Each topic is broken down into weekly lectures (3 lectures per week) that are arranged topically. Included are supplementary materials related to each lecture.

 

Topics Covered

Below are the mathematical subjects covered over the course of a 10-week course.

  • Introduction to MATLAB and programming
  • Linear Systems of Equations: Ax=b
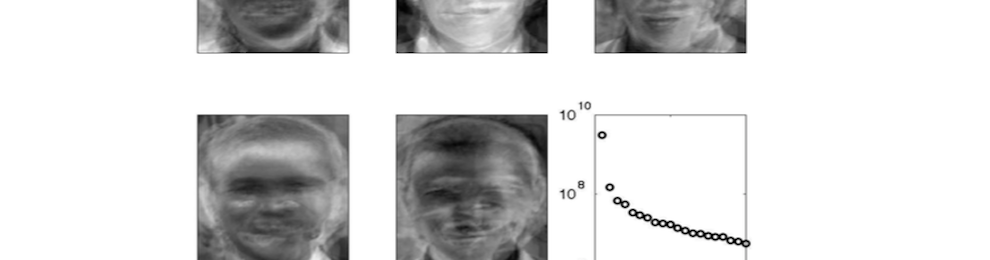
  • Singular Value Decomposition & Principal Components
  • Differential and Integrable Calculus
  • Differential Equations
  • Fourier Transform

 

 

Stacks Image 1145
© 2015 kutz