HYDROLOGY MODULE
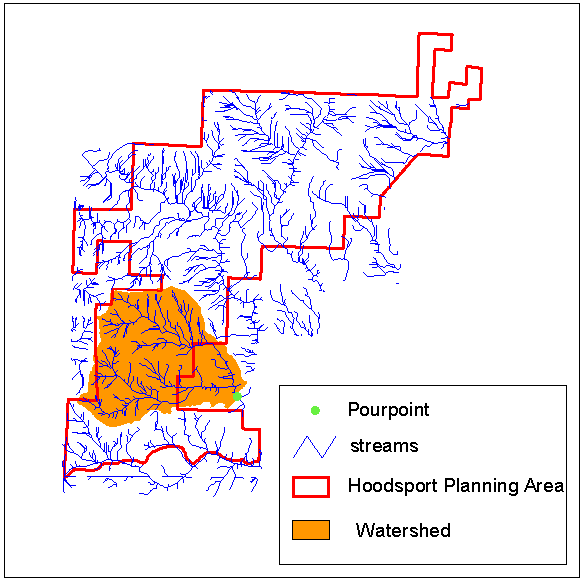
Hydrologic Change This hydrology module uses GRID analysis techniques to assess how road construction and stand management may affect stream discharge volume and timing. GRID is a raster or cell-based geoprocessing program that is integrated with Arc/Info (ESRI 1994). The baseline data sets that are needed for this analysis include a DEM (digital elevation model), a grid of the stream network, and a grid of the road system. The Washington State DNR (Department of Natural Resources) provided the data sets used in this hydrology module. Roads One way that roads affect hydrology is by changing the routing of the water within a basin. Roads alter hydrologic routing by changing where the water goes and how fast it gets there. Roads can also have a major impact on water quality and sediment loads, but those issues will be addressed in other modules. This module looks at how roads shorten flow paths and thus affect the timing of water delivery into stream channels. Road ditches capture most of the water that falls on a road surface or is intercepted by the road cutslope. Road cutslopes intercept water travelling through the upper soil layer. The amount of water a cutslope intercepts is proportional to the height of the cutslope and the volume of water draining through the soil layer. The standard culvert spacing on forest roads built in western Washington is approximately two hundred feet. A basic assumption of this module is that water flowing in a road ditch is transported across the road prism, through a culvert pipe, and delivered onto the slope below the road every 200 feet. Water flowing in a road ditch within 200 feet of a stream crossing is assumed to enter the stream directly. Flowlength can be defined as the distance a drop of water falling within a watershed must travel before reaching a stream channel. This module will assess the effect of roads on the routing of water by observing the change in flowlengths in the analysis watershed as road density increases. The analysis considers two levels of road density: no roads, and roads that are currently mapped in the watershed. Timber Harvest The most significant hydrologic effect of timber harvest in the Pacific Northwest Cascades is on snow accumulation and snowmelt rates during rain-on-snow events. Peak snow accumulation is reduced under forest canopies because tree canopies intercept snowfall and snow caught in the canopy is more susceptible to melt and evaporation. Rain-on-snow (ROS) events are large warm windy rainstorms that occur fairly frequently during the winter in western Washington. ROS events have been associated with some of the largest and most damaging floods on record because during ROS events heavy rainfall is combined with very fast snowmelt rates. Warm strong winds and high humidity are the conditions responsible for high rates of snowmelt during an ROS event. The wind transfers large amounts of latent and sensible heat into the snowpack. For example, when 1 inch of water is condensed from the vapor to the liquid state, 1500 calories are released. Only 200 calories are needed to melt 1 inch of snow water, which means that for every inch of water condensed onto the snow surface, 7.5 inches of snow water is melted. This module looks at the effect of timber harvest on snow accumulation, snowmelt during ROS events, and water available for runoff (WAR). The methodology follows the Hydrologic Change Module in the Washington Forest Practices board manual: Standard Methodology for Conducting Watershed Analysis, version 2.1, 1994. Site Description Analysis Watershed Figure 1 shows the location of the analysis watershed with respect to the Hoodsport planning area. The outlet of the watershed is the bright green point. The watershed includes the North and South branches of John's Creek.
Figure 1. Analysis watershed within the Hoodsport planning area. Methods Although the effects of road construction and harvest in a basin are integrated with respect to their impacts on peak flows, in this module, for analysis purposes, they are considered separately. Roads Flowlength (basin) The flowlength from each cell in the analysis watershed to the nearest stream channel is computed with the GRID flowlength function. The flowlength function requires a flowdirection grid. A flowdirection grid is a grid of the direction of flow across the land surface and is created from the dem with the GRID flowdirection function. Before running the flowdirection function, any sinks (areas of internal drainage) in the dem should be filled with the GRID fill command. The flowlength function computes the downslope distance from each cell in the watershed to the closest NODATA cell. Therefore, to create a flowlength grid to the nearest stream channel, all cells in the input grid must have a value except for the streamcells, which must be NODATA. The values of streamgrid must be transformed in order to be used as an input grid for the flowlength function because the values of streamcells in the streamgrid are equal to 1, while all other cells are NODATA. The streamgrid can be transformed with the GRID isnull and setnull functions. First the isnull function is used to convert the NODDATA cells to 0, then the setnull function is used to convert the streamcells to NODDATA. Flowlength (contribution to streams) The average flowlength of the contributing watershed area is computed for each stream cell using the GRID flowaccumulation function. The flowaccumulation function creates a grid of accumulated downslope flow into each cell. The flowaccumulation function requires a flowdirection grid and accepts a weight grid as an optional argument (Arc help). A grid of the average contributing flowlength to each stream cell is created by:
Roads that intersect the stream network effectively increase the drainage density of a watershed (stream length/basin area). Before starting each flowlength analysis, the intersections of the roads with the stream network are identified and 200 feet of road on either side of crossings are added to the stream network. The flowlength analysis described above is repeated for each level of road density. The change in flowlength due to road construction is found by subtracting each flow length grid created for a level of road density from the corresponding unroaded flowlength grid.
Harvest The harvest aml carries out the hydrologic analysis (described in detail below) and creates grids for an uncut and a clearcut basin. To compare results between the two basin conditions, grids for the uncut basin are subtracted from the corresponding grids for the clearcut basin. The harvest aml is interactive. The user must specify the following:
The grids created by the harvest aml are named with the convention shown in Table 1.
Table 1. Naming convention for the grids created by the harvest aml Snow Accumulation Average snowfall for the watershed is estimated as a function of elevation and canopy closure with equation (1): (1) snowfall = d1 + (d2 x E) d1 and d2 are the regional coefficients that can be found in table C-3 in the DNR handbook. The Hoodsport planning area falls in the Rain Shadow region. For this region, d1 = -0.357 and d2 = 0.02029. E is the mean elevation in meters. To model an unusual snowfall, the standard error of the estimate (SEE) is added to the average snow accumulation: (1a) snowfall = d1 + (d2 x E) + SEE Equation (2) modifies the amount of snow estimated by equation (1) to account for variations in forest canopy. (2) SWE = snowfall * R R , the snow water equivalent ratio, can be calculated with equation (3). (3) R = 1 + 2 * ((1500-E)/1500) * (1-F) E is the elevation in meters, F is the fractional canopy percent.
Snowmelt Snowmelt potential is calculated with the U.S. Army Corps of Engineers (1956) snowmelt equation: (4) SM = T (0.133 + (0.086 * U) + (0.0126 * P)) + 0.23 SM = snowmelt (cm water), T = temperature (°C), U = windspeed (m/s), P = precipitation (cm/24 hr) Snowmelt potential can be calculated for an 'average' storm or an 'unusual' storm Temperature is determined from a generalized regional lapse equation: (5) T = 8.1 - (0.006 * E) For an unusual storm, 2° C is added: (5a) T = 8.1 - (0.006 * E) + 2 Windspeed (Uc) is estimated from a wind speed frequency curve found in the DNR manual; then it is corrected for forest cover with equation (6) (Dunne and Leopold 1978): (6) U = Uc (1-(0.8 * F) For an average storm Uc equals the wind speed that is exceeded 50% of the time; for an unusual storm Uc equals the wind speed exceeded 16% of the time. The precipitation recurrence interval and amount of precipitation in centimeters for the 24 hr storm must be entered by the user. Precipitation values for the 2-year 24-hour storm used in this module were taken from a Western US Precipitation Frequency map published in the 1973 NOAA atlas.
Water available for runoff Water available for runoff (WAR) is calculated by adding snowmelt (4) and precipitation. (7) WAR = SM + P The snowmelt grid (SM) is actually the snowmelt potential, so if the value for SM is greater than the snow accumulation (SWE) then SWE is used in place of SM in the equation. (7a) WAR = SWE + P
WAR accumulation The GRID flowaccumulation function is used to model the downslope accumulation of the water produced by the rain-on-snow event (WAR). The model assumes instant delivery and 100% conservation of the 24-hr volume of water. This module does not address flow routing or water loss through storage or evapotranspiration. (8) WAR-accumulation = flowaccumulation(flowdir,WAR) The WAR-accumulation grid results can be limited to stream cells with the GRID con function to show which stream reaches are affected the most by changes in WAR-accumulation due to harvest. (9) stream-WAR-accumulation = con(stream cells, WAR-accumulation) Stream discharge (not included in the aml) The 'describe' grid command is used to get the maximum value of WAR accumulation for the cut and uncut watersheds. This maximum value is the total WAR produced by the 24-hour storm within the analysis basin. Depth of water is converted to a volume by multiplying the maximum accumulated WAR by the area of a single grid cell. Volume is converted to discharge by the relationship 1cfs/day = 1.98 acre-ft. Basin discharge is estimated with the USGS regional regression equation: discharge = function (basin area, annual precipitation)
Watershed statistics are displayed in Table 2
Table 2. John's Creek watershed statistics
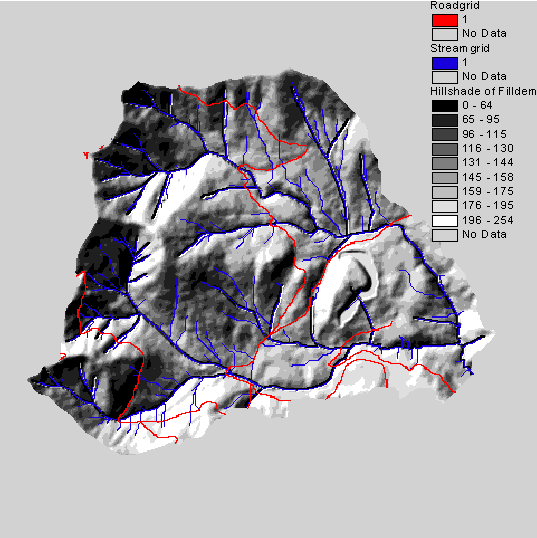
Figure 2 shows an image of the analysis watershed with the stream network and current transportation system.
Figure 2. Hillshade of filldem, roadgrid and streamgrid
Roads Figure 3 shows the flowlengths (flow distance from each cell to the nearest streamchannel) in the basin without roads.
Figure 3. Flow length grid - basin with no roads
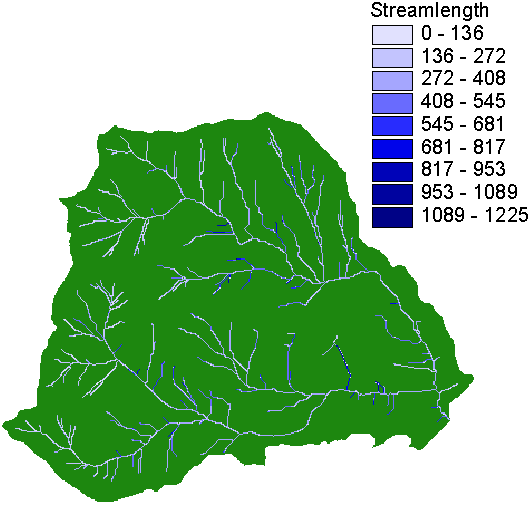
Figure 4 shows the average distance water must travel to reach each stream cell in the basin without roads.
Figure 4. streamlength grid
Figure 5 shows the areas of the basin where flow length has shortened due to roads
Figure 5. change in flowlength grid
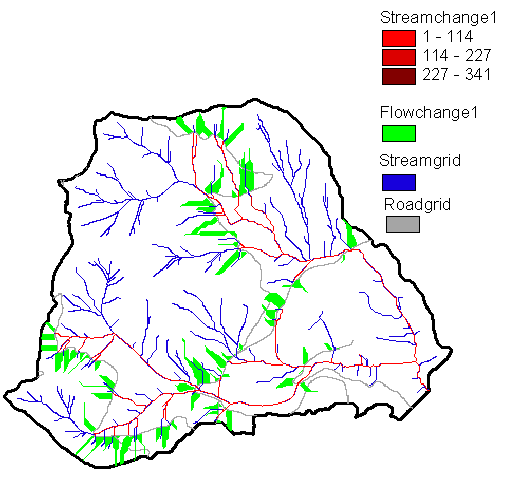
Figure 6 is an image showing the change in the average flowlength of the contributing watershed area to stream cells. The red stream cells have had their average contributing flowlength shortened by roads.
Figure 6. changes in basin flowlength(green) and changes in average flow length contributing to streams (red)
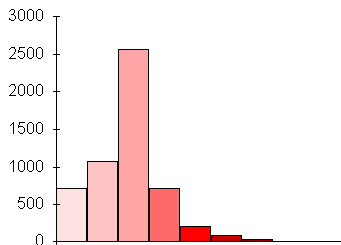
The histograms of the 'average-flow-distance-to-stream-cell' between the unroaded and roaded basin are compared in figure 7. The number of cells in the lowest 'average-flow-distance-to-stream-cell' category increased from 750 in the watershed without roads, to over 1000 in the roaded watershed.
Figure 7. Histograms of the average flow distance to stream cells for basins with no roads and with roads.
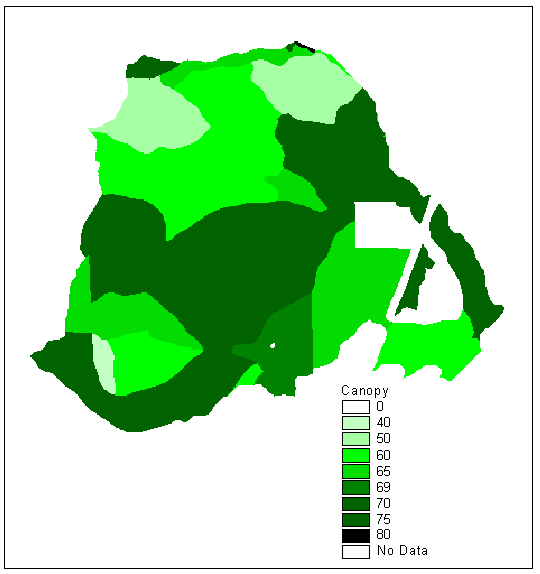
Rain-on-Snow Figure 8 is an image of the percent canopy closure of the uncut basin
Figure 8. Uncut canopy closure grid
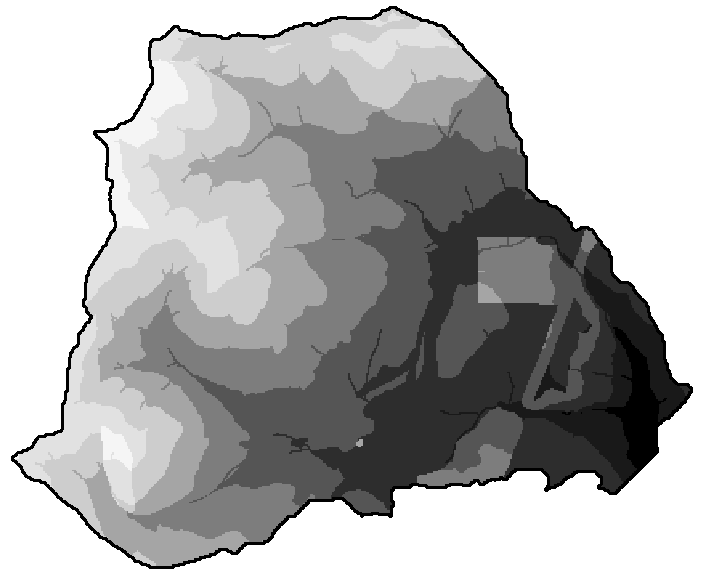
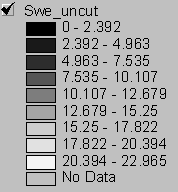
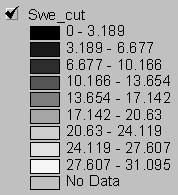
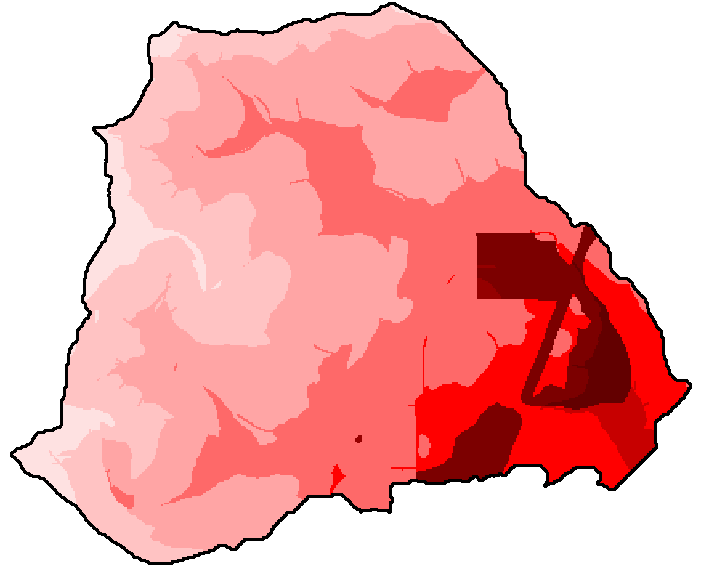
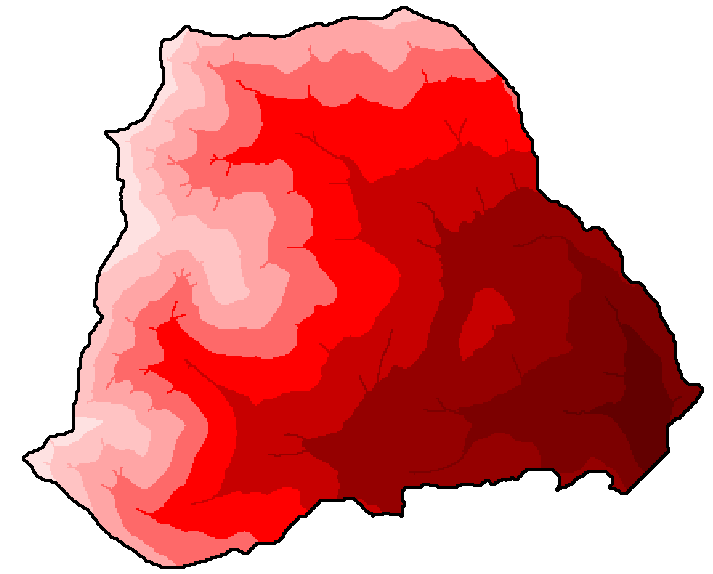
Snow accumulation grids for the uncut and clearcut basin are displayed side by side in figure 9 for comparison. Lighter shades of gray correspond to greater SWE. The maximum snow accumulation (SWE) for the cut and uncut basins is 12.2 inches and 9.0 inches respectively.
Figure 9. SWE grids for uncut and clearcut conditions
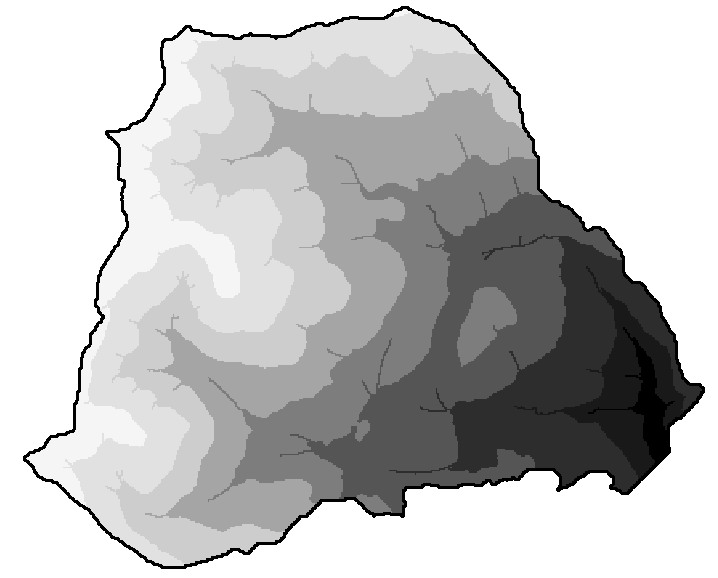
Figure 10 shows the difference in snowmelt potential during a 24 hour 2yr rain-on-snow event for the uncut and clearcut watersheds. Darker red corresponds to higher snowmelt potential. Snowmelt potential for the design storm ranges from about 0.5 inch to 2.4 inches for both basins,
Figure 10. Snowmelt grids
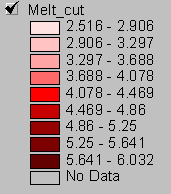
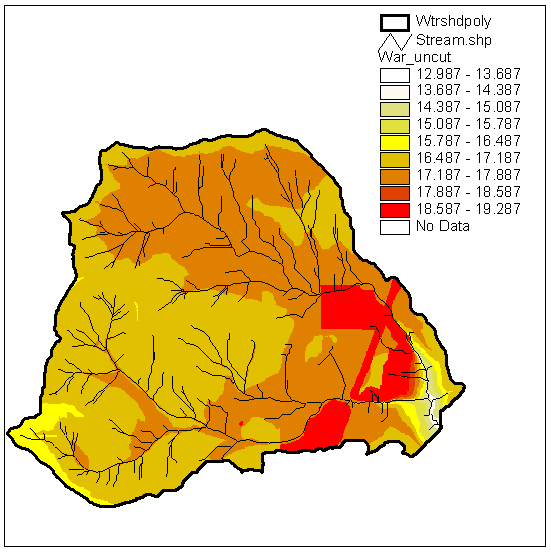
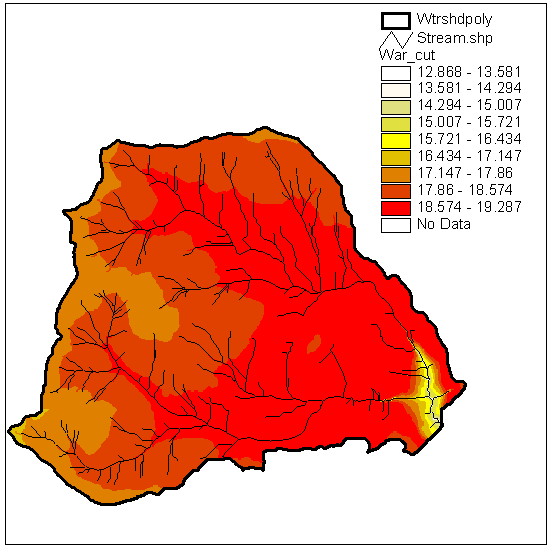
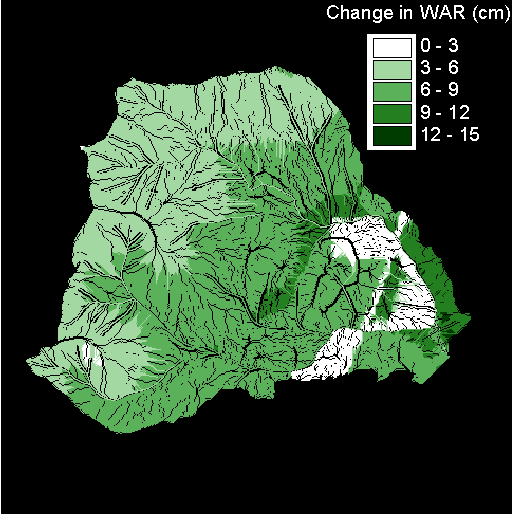
Figures 11 and 12 show the difference in water available for runoff (WAR) between the uncut and clearcut watersheds. The range in WAR over the basin produced by the storm for both harvest levels is about 2.5 inches (from 5 to 7.5 inches).
Figure 13 shows the percent difference in WAR accumulation between uncut and cut watersheds.
Percent change in downstream accumulation of WAR between uncut and clearcut basins is shown in figure 14. Reaches can be designated as low, medium, or high risk depending on the magnitude of change caused by cutting.
Figure 14. Percent change in WAR reaching stream cells from uncut to cut condition.
Stream Discharge Table 3 shows the total WAR for the cut and uncut basins and the difference between the two.
Table 3. Maximum accumulated WAR
The basin area was computed using zonal area grid function on the watershed grid. Grid: area = zonalarea(watershed) Basin area = 100965944 square feet Converting to acres: Basin area = 100965944 / 43560 sq ft per acre = 2317.9 acres Calculating the difference between the two basins in acre-ft of water for the 2-yr 24-hour storm: 3593.5 ft * 32.823 ^ 2 square ft/ 42560 square ft/acre = 5.41 acre-ft. This is the unit-averaged difference in WAR. Acre-ft for a 24 hour period can be converted to cfs by the relation 1 cfs/day = 1.98 acre-ft 5.41 acre-ft / 1.98 = 2.73 cfs difference as basin outlet (contributed by 24hr 2yr storm) between the cut and uncut watershed. USGS regional regression equation to estimate a ballpark basin discharge for the basin: Q = a * Ab1 * Pannb2 Pann = average annual precipitation inches = 80 A = basin area in square miles = 3.62 a, b1, and b2 = regional coefficients = 0.104, 0.86, and 1.51 Q = 0.104 * 3.62^0.86 * 80^1.51 Q = 235 cfs Ballpark estimate of percent increase in discharge from clearcutting during a 2-yr 24-hr ROS event is = 1.2 percent Discussion Roads The results of the hydrologic road density analysis show that roads, by intercepting throughflow, can dramatically shorten the distance that water must travel before reaching a stream channel. The maximum flowlength change in this small watershed is over 1000 feet. The module is instructive because it demonstrates that the total length of road is less important in changing flow routing than is the number of stream crossings, whether the road slopes toward the stream at these crossings, and the culvert spacing. Most working models must make some simplifying assumptions. The basic assumptions of this module are:
The effect of roads on flow routing is probably greater than this module indicates, because the influence of roads on flow volume and flow rate is not addressed. The module assesses the timing of the delivery of water to streams in part, by measuring flowpath lengths, but does not take into account how roads increase flowrates. Water intercepted by roads, either directly or through cutbank interception, travels very quickly compared to water moving through soil. In addition, the model assumes that once the water is discharged onto the fillslope, it infiltrates into the soil and continues to move downslope as throughflow, which may or may not be the case. Roads also influence the total volume of water delivered to stream channels. A large percentage of the water infiltrating the soil during a rain storm or snowmelt event is stored there or evapotranspired. When throughflow is intercepted by a road, a greater percentage of the total volume is conserved and delivered to stream channels because the water moves quickly over a poorly vegetated almost impermeable surface. Throughflow, intercepted by cutbanks, accumulates in the road ditch until discharged into a stream channel or onto the fillslope by a crossdrain outlet. The wider the culvert spacing, the more water is intercepted and accumulated in the ditch, and the more flow is concentrated at the culvert outflows. High discharge from culverts increases surface erosion and mass wasting potential by eroding and saturating slopes. If water is kept off the road surface and does not overflow the road ditch, the culvert spacing is small enough to prevent road deterioration, but still may not be small enough to prevent environmental consequences from concentrated flow. Harvest Results from this module can best be interpreted by looking at the relative change in discharge between different levels of harvest for storms of similar frequencies (Watershed Analysis manual 1994). More WAR produced during a given frequency storm should increase discharges and shift flood frequency curves. Module results show a 6.8% increase in WAR produced for the 2yr 24-hour storm in the clearcut basin from the uncut basin. This increase is only about 1% of the estimated average basin discharge. The small change in runoff from clearcutting the John's Creek basin could be due to the low elevation of the basin (125-2700 ft) and the small basin area (3.62 square miles). If a larger basin at a higher elevation were clearcut, the larger downslope accumulation of WAR would probably result in greater percent increase in stream discharge. Also, this hydrologic analysis was run for the 2-yr, 24-hour precipitation event and for average snowfall conditions and an average storm intensity. If the analysis was repeated for a larger more intense storm, the relative change in discharge between the two harvest levels may be greater. The equation used to convert WAR to stream discharge assumes that 100 percent of the water from rain and snowmelt is delivered instantly to the basin outlet. The equation does not include a term for the time it would take for the water to travel to the basin outlet or a term for the volume of water lost in transit. Since much of the water available for runoff enters the soil and is stored there or used by plants, the actual volume of water delivered to the outlet in both the cut and uncut watersheds would be lower than the module predicts. On the other hand, the relative difference in peak flows between the uncut and cut basin would probably be higher than is indicated by the difference in WAR because travel time for the WAR would be less in the clearcut basin. Travel time is lower in the clearcut basin compared to the uncut basin for two main reasons. First, road density is higher. As discussed earlier in this report, roads shorten the average flow length and increase flow speeds. Second, transpiration rates are lower in a clearcut basin. Less transpiration results in wetter soils. Water travels faster in wet soils than in dry soils and if the infiltration rate is exceeded, overland runoff occurs. Many ROS events last longer than two days, and once the soil becomes saturated, a much higher percentage of the WAR will reach stream channels. Assumptions and Uncertainty The methodology of the harvest portion of this module is based on the assumption that "the greatest likelihood for causing significant, long-term cumulative effects on public resources via alteration of forest hydrologic processes is through the influence of timber harvest on snow accumulation and melt during rain-on-snow (ROS) storm events" (Watershed Analysis manual 1994). The amount of meteorological data necessary to run a physically based model for snow accumulation and melt is very large. Because few analysis watersheds have this data available, the DNR methodology uses an empirical approach, relying on regional equations to estimate baseline snow accumulation, storm parameters (temperature, windspeed, precipitation), and melt rates. There is a large degree of uncertainty associated with the results. For example, to get from estimates of snow accumulation to estimates of water available for runoff (WAR), the methodology uses a total of 6 empirical equations, each with its own set of assumptions and degree of uncertainty. Error increases with each step in the process because each successive equation uses the results from previous equations.
Participating in the watershed analysis process is an effective education in watershed dynamics, both the physical and biotic components, and how they interrelate. For example, harvest increases snowpack accumulation and melt, resulting in greater storm runoff and stream discharge. This, in turn, increases mass wasting hazards and surface erosion and affects channel processes and fish habitat. The watershed analysis procedure directs our attention to the critical questions that must be answered in order to confidently evaluate and compare different land use management plans. We quickly become aware of the gaps in our knowledge and in our data. Working through the modules using real and less than ideal data sets demonstrates the difficulty of quantifying environmental processes such as surface erosion, mass wasting, stream discharge, etc. These processes are difficult to quantify because the ecosystem is not a closed system. Rather, it is complicated, highly variable, and unpredictable. More complex models may better represent reality, but a drawback of using them is that they require extensive data sets that are costly in both time and labor to collect and assemble. The data sets required to produce an accurate and reliable assessment of basin conditions and to predict effects of land management are currently unavailable, and perhaps even unknown. With limited data available, it may be better to stick with simple models. GIS-based watershed analysis is a fast effective way to compare the relative environmental impacts from various harvest plans and transportation systems. Model output does not have to be strictly accurate as long as relative comparisons hold. Another benefit of using GIS is that the powerful spatial analysis capability of GRID can quickly locate areas of high environmental risk, which can prevent hours of wasted time by focusing field efforts in high-risk areas.
|