-Mass Wasting-

Hoodsport Watershed Analysis

By Susan Seaberg

Introduction

Methods

Results and Discussion

Conclusion

References

Mass Wasting AML

 

 

 

 

Introduction

The Mass Wasting module will estimate the possibility of a hill slope failure and whether the sediment will be delivered to the stream network. Mass wasting or landslides occur naturally in every environment, although some may occur prematurely due to human activities. The objective for this module is to locate areas where landslides are more probable to occur and isolate the factors that may attribute to early activation of the mass wasting events. Many factors can be attributed to landsliding events including the internal properties of the soil structure, vegetation, topograhy and water.

Figure 1. DEM and stream layer for the project area.
 

The soil structure is based on how the soil was formed. Soils are decomposed materials and disintegrated rock of many different mineral compositions. This mixing of components will give each soil type a structure that will enable the particles to hold together yet allow some water and air to pass.

The analysis for the mass wasting was performed by writing an analysis program for Grid in Arc/Info using the Arc Macro Language (AML). The mass wasting aml created was used with the soil coverage, dem and stream layer. Figure 1 shows the dem with the stream coverage atop.

 

Methods

The mass wasting analysis that was conducted included the use of three different methods: the Shaw Johnson method and Infinite Hillslope equation. The Shaw Johnson method analyzes the mass wasting hazards using the curvature of the land surface and the steepness of the slope. The Infinite Hillslope equation is a more complex analysis based on the slope, soil properties including cohesion, saturated unit weight and the internal angle of friction, soil thickness, saturated soil thickness and root cohesion.

Shaw Johnson

The Shaw Johnson method utilizes the concavity of the topography in combination with the local slope in determining areas of mass wasting hazards. Table 1 explains the relationship of the inputs with respect to the rating output.

 

Table 1. Shaw Johnson approach to mass wasting hazards. The analysis is based on concavity and local slope.
 

Slope (%)
 Curvature

 0-15

 15-25

 25-47

 47-70

 > 70
 CONVEX

 Green

 Green

 Green

 Green

  Yellow
 PLANAR

 Green

 Green

Green
     Yellow

  Red
 CONCAVE

 Green

   Yellow

 Red

  Red

  Red

This method was used in the Hoodsport watershed analysis to locate general areas of mass wasting hazards. Due to the analysis using only two variables for prediction, this method should not be the only possibility in hazard ratings.





  
Infinite Hillslope





The Infinite Hillslope Equation is a better analysis of mass
wasting potential. This equation utilizes more variables that
are more closely attributed to landsliding events. These variables
include the soils properties, soil depth and saturated depth as
well as local slope and vegetation. The outcome of the Infinite
Hillslope Equation is a factor of safety that can be used to estimate
the potential for failure. The factor of safety is essentially
a ratio of the resisting forces within the soil to the downslope
forces. A factor of safety < 1 will identify those slopes that
are more likely to fail than slopes with a factor of safety >
1. The equation is:



FS = Cs + Cr + (q0 + h*g sat - g w *
z) * tan(f ) * cos2(q
) / (q0 + h*g
sat) * sin(q ) * cos(q
)




  

    

      

        

          

            
where, FS = Factor of Safety
Cs = the Soil Cohesion
Cr = the Cohesion due to Roots
q0 = the Surcharging Weight of Vegetation
h = the Soil Thickness
gsat = the Unit Weight of Saturated Soil
gw = the Unit Weight of Water
z = the Saturated Soil Thickness
f = Soil Friction Angle
q = the Slope

          

        

      

    

  





 



When this equation was used in the analysis, many of the variables
were not singular values but a range of values for certain variables.
With the soils layer that we received from the DNR, many of the
variables were not included and the soil descriptions were very
vague. As I mentioned in the Soils
section of the Hoodsport Watershed Analysis, many of the properties
were estimated for a range of values. Using the ranges of values
for many of the variables a series of mass wasting potential grids
were created. During the analysis of the factor of safety grids
some variables were manipulated, some were controlled and some
were held constant. Table 2 is a summary of the variables and
their roles in the analysis.



 




  
Table 2. Factor of Safety Inputs. Variables in the
analysis that are controlled, systematically manipulated and held
constant.

   
  

    
    
Minimum or Maximum Values Used

    
    
 Systematically Varied Values

    
    
 Variables Held Constant

  

  

    
    
 Phi

    
    
Root Cohesion

    
    
 Surcharging Weight of Vegetation

  

  

    
    
 Saturated Unit Weight

    
    
 Soil Cohesion

    
    
 Theta

  

  

    
    
 Soil Thickness

    
    
 Saturated Soil Thickness

    
    
 Unit Weight of Water

  





 



Eighteen grids were created for the analysis. Six grids were
created for the using the minimum
values in the above table, six grids were created using the
maximum
values and six grids were created using random
variables within the variable range for the miniumum/maximum
values and the systematically varied values.



Two additional grids were created for the average of the eighteen
grids created. One of the grids used an integer average and the
other used a floating point average. The difference between these
two grids is that the failing areas on the integer grid were areas
that failed in all eighteen grids while the floating point average
grid creates a range of failure based on how many times that area
failed in the eighteen grids.



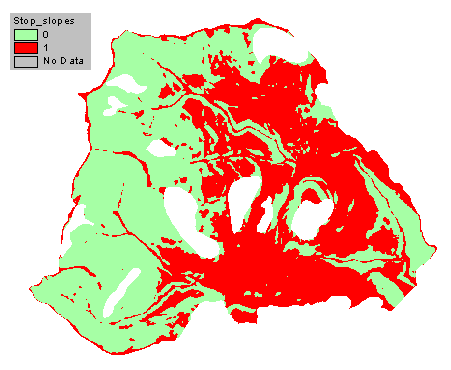
The delivery of potential mass wasting events to the stream
network was estimated based on the soil's internal angle of friction.
We estimated that a mass wasting event would stop if it reached
a slope that was half as steep as the internal angle of friction.
Any streams that were located within the area of non-stopping
slopes were more likely to transport the sliding soil mass further
downstream if a failure was to occur then streams located within
stopping slopes.



 



Results and Discussion



The mass wasting hazards were estimated using two methods,
the Shaw-Johnson approach and the Infinite Hillslope equation.
The Shaw-Johnson method utilizes the slope and the curvature of
the land surface and provides an initial estimate for areas of
mass wasting hazards. The Infinite Hillslope equation is a more
complex analysis using many specific soil properties including
the saturated unit weight, internal angle of friction and soil
cohesion, the soil depth, saturated soil depth, root cohesion,
surcharging weight of vegetation and the slope providing a better
estimate for mass wasting potential.



Figure 2. is the output for the Shaw Johnson covering the project
basin within the Hoodsport watershed, green areas are more stable,
yellow areas have a moderate hazard rating and red areas, located
where the slopes are much steeper and more concave, are the areas
of greatest mass wasting hazards.




  
Figure 2. Shaw Johnson Analysis in the Hoodsport Watershed Analysis. 
The approach analyzes concavity and local slope for hazard ratings. Green areas
are stable, yellow areas have a moderate hazard and red areas have a high hazard.


  

    
    
 

  





 



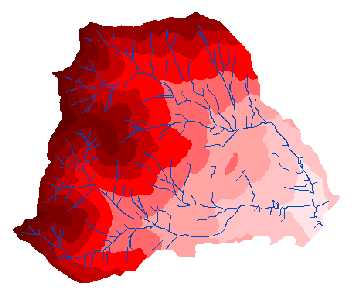
The Infinite Hillslope equation was used for a better estimate
of mass wasting probability. Eighteen grids were composed for
the analysis. Six were created using minimum
values, six for maximum
values and six created using random
values within the range of each variable. Once all of these
were created, two average grids were made. One average grid was
an integer average and the other was a floating point average.
The integer average grid, figure 3, shows the areas where failures
occured in all eighteen grids, while the floating point average,
figure 4, shows the range of failures. In the floating point average
grid, darker red areas failed in more of the grids than the lighter
red areas where failures may have only occured in a few grids.
The areas with no color were rock outcrops located within the
basin. These areas were taken out of the analysis leaving islands
where no mass wasting would occur.



 




  

    
    


    
Figure 3. Factor of Safety integer average grid. Areas in
    red failed in all eighteen factor of safety grid.
 
    
    


    
Figure 4. Factor of Safety floating point average grid. Areas
    in red failed in the eighteen factor of safety grids created.
    The darker red areas failed more than the lighter red areas.
 
  





 



If a mass wasting event were to occur, a logical question would
be what would it affect? We estimated that if a mass wasting event
were to occur, it would stop if it encountered a slope htat was
half as steep as the soils internal angle of friction. Figure
5 shows the areas where mass wasting would stop (red) and areas
where they would not stop (green).




  
Figure 5. Mass wasting stopping slopes. Mass wasting
events that would occur in the green areas will not stop, but
once they would stop once they encountered the areas in red.

   
  

    
    
 

  





Based on these stopping slopes, the streams that would be affected
were located. If a stream was located in a non-stopping area,
it was assumed that if there was a mass wasting event that occured
in the proximity of the stream it would be delivered to the stream
network and transported downstream. Figure 6 shows the areas of
the streams that would be potential delivery sites of mass wasting
events.




  
Figure 6. Delivery streams. Portions of the stream
network located within the non-stopping slopes (red areas) would
be areas of potential delivery.

   
  

    
    

  





Utilizing the stream locations within the delivery areas and
incorporating the mass wasting potential enables the creation
of potential a potential mass wasting delivery grid, figure 7.
This grid analyzes the mass wasting zones within proximity to
the stream network for potential delivery.




  
Figure 7. Mass wasting delivery. Mass wasting potential
areas incorporated with the stream network for analysis of potential
delivery.

   
  

    
    

  





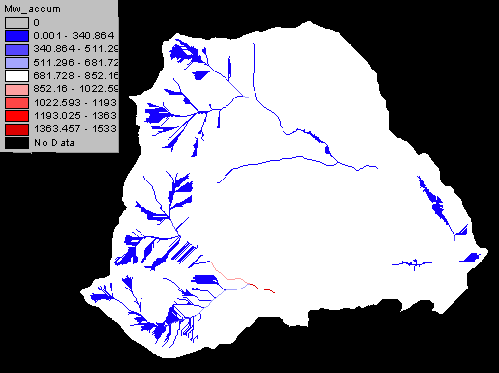
Further analysis for the mass wasting delivery potential led
to the grid of mass wasting accumulation into the stream network.
Figure 8 accumulates the potential for mass wasting to occur through
the stream network.




  
Figure 8. Mass wasting potential accumulated into
the stream network. Increased mass wasting potential develops
into more delivery down the streams.

   
  

    
    

  





Areas where more mass wasting occurs impacts the streams by
increasing the sediment delivered down the streams.



 



Conclusion



Within the basin of analysis, there are not many areas where
landsliding will be an imminent problem. The areas prone to any
mass wasting events occur in the steeper slopes of the basin where
human activity will most likely occur in the more distant future.



 



 



References



Dunne, Thomas and Leopold, Luna, Water in Environmental
Planning, Freeman and Company, New York, 1978



United States Department of Agriculture, Forest Service, Level
I Stability Analysis (LISA) Documentation Version 2.0, April
1992



Official
Soils Series Descriptions-USDS-NRCS Soil Survey Division



Soil Texture
Triangle: Hydraulic Properties Calculator



 Krogstad, Finn, Personal Interview, February to March
, 1999