Introduction to Geographic Information Systems in Forest Resources
| Introduction to Geographic Information Systems in Forest Resources |
|
|||||||||||||||
|
|||||||||||||||
As is the case with any data relating to a location, scale is a critical issue in GIS. The scale of a map used for locating major watersheds within the Columbia River basin will be different than the scale of a map used for locating forest inventory plot centers within a single district in a National Forest.
If you are analyzing the spatial distribution of clumps of exotic shrubs, you might want to represent the shrub clumps as points. However, if you were analyzing the amount of ground covered by individual plants within those clumps, you might represent the plants as individual polygons. As you gain more experience, you will know what type of data to use to represent the feature you are studying.
Additionally, for any phenomenon that has a spatial component, there are also scale-dependent behaviors or properties. A typical example is animal migration. A salamander may have a relatively large territory (compared to the size of the animal itself), but that territory may be negligible in size compared to that of a brown bear sharing the same habitat. Relatively small disturbances in the salamander's territory might prove fatal to the salamander, but those same disturbances would probably go completely unnoticed to the bear.
There are no hard and fast rules for determining appropriate scales of data, but as you gain experience, you will become aware of when and why to use data of varying scales.
The essential problem of scale in a GIS is that all features are stored with precise coordinates (the computer stores numeric values), regardless of the precision of the original source data. Data which came from any mixture of scales can be displayed and analyzed in the same GIS project. The output of mixing data of differing scales can lead to erroneous or inaccurate conclusions.
Consider these two coordinates:
(125.875, 500.379)
(126.000, 500.000)Both coordinates are stored with the same precision (3 decimal places). If we ignore the 3 decimal places of precision, the 2 coordinates are identical, but if we use the full precision of the data, the coordinates are different. Depending on the scale at which you view these points, they will either look like a single point or they will look like 2 separate points. As you zoom in closer, the relative distance between the points will increase.
Using data from many different scales introduces these types of problems. The adage "A chain is only as strong as its weakest link" applies here; the accuracy and precision of measurements, maps, and models from a GIS are only as good as the least accurate and precise data source.
While scale issues in GIS are problematical and need to be addressed, we do not have the time for a full treatment. Instead, presented here are a few examples to demonstrate the effect scale can have on GIS.
How large are features?
You should be careful with the original source scale for features in the GIS. The real-world size of features may not be correctly represented within the GIS. Consider these examples.
A line drawn on a map may look thin, but the real-world feature may actually take up area (width) on the ground. A dot on the map (e.g., an airport or city) occupies area on the ground.
For example, a line of width .025" on a 1:24,000 scale map will have a width of 50' on the ground.
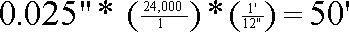
Consider this problem: you would like to characterize a the forest stands within a planning area by the amount of annual precipitation. Your forest stand dataset came from orthocorrected 1:2,400 aerial photographs, and is highly accurate and precise. But the only precipitation data you could find were from a statewide, 1:2,000,000 scale source.
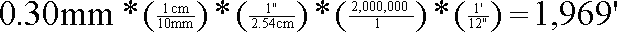
The thinnest line on the precipitation source map (0.30mm) is in actuality nearly half a mile wide on the ground! The 1/2 mile error only takes into account the error implicit in the map symbology. You should also consider the error in the precipitation model itself. How were the precipitation isohyetals originally developed? Where were the sampling stations? Who was responsible for drawing the lines?
When you view both datasets in the GIS, they will have the same apparent precision (that is, both lines look like hairlines on the screen), but in reality, the precipitation data are far less precise than the forest stand data. What implications could this have for your analysis?
The same problems of scale will exist when mixing either vector or raster data from different scales.
Scale statements
What is the difference between "large scale" and "small scale" in maps? Large-scale maps cover less ground on a page of an equal size small-scale maps. Examine the reason for these names; the scale's representative fraction is relatively large or small.
A number of 1/24,000 is smaller than a number of 1/4,800. The former says "One unit on the map is equal to 24,000 units on the ground." The latter, "One map unit equals 4,800 ground units."
| 1/24000 |
1/4800 |
| smaller numeric value | larger numeric value |
| smaller scale | larger scale |
It may take you a while to get comfortable with this terminology, but it is something that you will eventually need to know intuitively if you keep working with GIS. One way to remember this is that the same feature on a small-scale map will appear smaller than the same feature on a large-scale map.
What features & details exist at different scales?
Scale will affect not only analytical functions, but also map display. The smaller a map's scale (i.e., the more ground area it covers on a page), the more generalized the map's features are. A road or stream that is quite sinuous on the ground may be represented by a fairly straight line on a map. Sometimes features are dropped altogether from smaller scale maps.
Here is an example of data captured at several different scales. The shaded polygon is Pack Forest's administrative boundary.
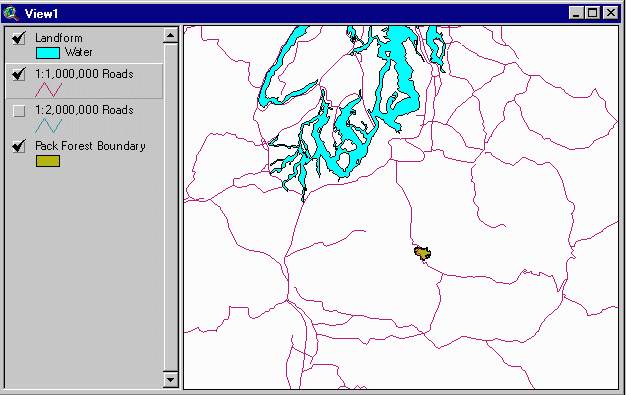
(Data from the Digital Chart of the World, from source data at a scale of 1:1,000,000)
(Data from the USGS, from source data at a scale of 1:2,000,000)
Notice how the 1:1,000,000 details differ from the 1:2,000,000 scale roads. Apart from the difference in scale, each dataset was developed to meet a different need. USGS data is developed for multipurpose map use, whereas the DCW data were developed primarily for military uses.
Compare these smaller scale data to a considerably larger scale data source (USGS 1:100,000 scale digital line graph):
(Data from the USGS, from source data at a scale of 1:100,000)
Representative fraction or unit conversion?
Different professions use different terminology to represent scale, and you should be aware of any conventions in your industry.
It is common for foresters and other natural resource professionals to use terminology such as "one to 2000," meaning "one inch on the map represents 2000 feet on the ground."
Geographers and professionals in other disciplines use the same terminology, but "one to 2000" means "one inch on the map represents 2000 inches on the ground."
Be careful when you communicate scale fractions to personnel outside your particular field of interest: to a forester, the "one to 2000" map is the geographer's "one to 24,000" map!
For this course, all scale statements are assumed to be unit-to-unit unless specifically otherwise stated.
Return to top | Ahead to Help Topics
|
|||||||||||||||

|
The University of Washington Spatial Technology, GIS, and Remote Sensing Page is supported by the School of Forest Resources |
School of Forest Resources |