TAPESTRY: The Art of Representation and Abstraction
Transformation: Mirror, hand, reverse, flip
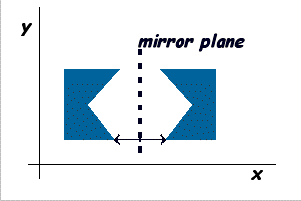In a mirroring or reflection operation, a shape is "flipped over" the mirror line (2D) or plane (3D). Each point in the original is repositioned relative to the mirror line/plane, ending up an equal distance away, but on the opposite side.The easiest mirror operation uses one of the primary coordinate system axes as the plane and simply multiplies all x coordinates (or all y-coordinates, or z-coordinates) by -1.
More general mirroring operations usually rely on the user selecting or indicating a line (or plane) in space. Because a line is somewhat easier to establish than a plane, a line is sometimes used, assuming that the mirror plane is perpendicular to the line, passing through it's midpoint.
Topologically, mirroring turns objects inside-out, so programs maintaining consistently ordered surface orientations must compensate for the inversion by reversing the ordering of the faces which have been mirrored.
Last updated: April, 2014
