TAPESTRY: The Art of Representation and Abstraction
Data - Data Structure - Organization
What's it all about?
)
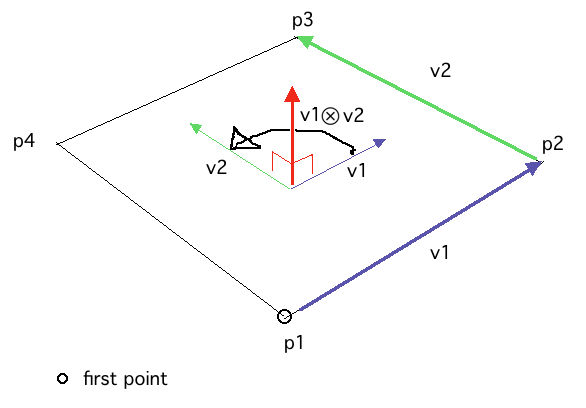The description of how surface normals are calculated ("Data > Surface Normals") describes the mathematical process for calculating surface orientation using two vectors (v1 and v2) derived from the vertex list of the polygon using the vector "cross product" to get a vector perpendicular to the polygon. For convex polygons such as the one shown at right, this process gives the same surface normal regardless of which vertext you start with (imagine moving the "first point", but keeping the ordering of points the same). This isn't always the case.
)
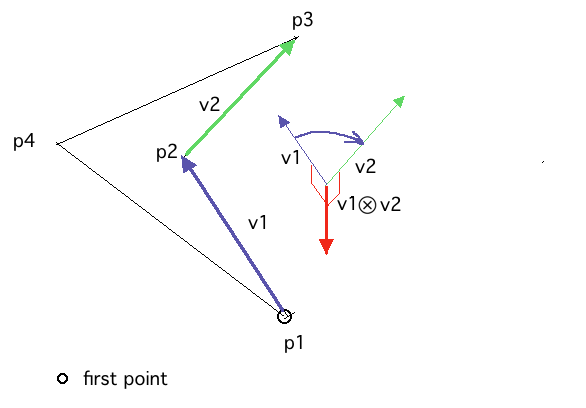If the polygon has a concavity in the boundary, the choice of "first point" matters. As shown here, it is possible that the cross-product will point in the opposite direction for some starting points. That's not good.
Programs may avoid this by always using triangles, because they can't be concave, or by providing an editing mechanism by which the first point can be manually selected, allowing the author to correct for errors such as this.
Last updated: April, 2014
