TAPESTRY: The Art of Representation and Abstraction
Path Tracing
BOTH ... AND ...
The simple rendering techniques (Gouraud, Phong, etc.) are able to render from the model to the screen by assuming a perfectly diffuse surface and limited transparency, while ray tracing renders from the screen back into the model by assuming a perfectly specular surface. Unfortunately, they are both wrong. Real surfaces are both diffuse and specular, in varying amounts, and are described by their Bidirectional Reflectance Distribution Function, or BRDF. Correctly dealing with this condition requires a "both ... and ..." approach to rendering.
Bidirectional Reflectance Distribution Function: BRDF
Where the specular assumption says there is a 100% probability of light reflecting at the same angle as the angle of incidence, and the diffuse assumption says there is an equal probability of light reflecting in any specific direction, the BRDF attempts to characterize it in a more nuanced way. The reflective character of a surface depends on the angle of incidence, but may also depend on the wavelength of the incident light, and any number of other factors. Collectively, these factors define a function that define an energy distribution (or a probability distribution) of light striking the surface.
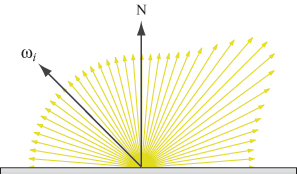We can visualize the BRDF as follows. If we draw our "BRDF reflection" showing that some light goes off in each direction, we might indicate how much goes in each direction by the length of the ray in that direction. Such a diagram would look like the one at right. For highly specular surfaces, the "outbound" curve is long and narrow, with the majority of light reflected off in roughly the same direction, approaching the perfect reflection. For very diffuse surfaces, there might only be a slight bulge. This un-eveness is what the BRDF captures.
Probabalistic rendering
The BRDF for a material only indicates that when light strikes the surface, some of it goes off in each of an infinite number of directions. Infinity is bad, so how can we use this fact? The answer is to take a probabalistic approach and ask about individual "rays of light" rather than "light" in general. As with coin-flipping experiments, if we do the thing ("sample" the phenomenon) enough times, we should find that the observed behavior approaches the theoretical behavior. So, if we "sample" the scene (or a single pixel in the scene) enough times, we should be able to get a correct rendering, even when the individual light rays are individually assigned to one bounce angle or another based on the BRDF. Ray tracing samples the scene once per pixel, using the deterministic specular assumption. Path tracing makes one or two changes to this approach.
Each time a ray intersects a surface, we can use the BRDF to randomly select a direction for the ray to bounce (sometimes called "Monte Carlo" ray tracing because Monte Carlo is where a lot of gambling takes placed, and thats all based on probability... ). If a ray bounces around a few times and hits a light source, then that ray contributes to what we see in the scene. If not, then it doesn't. If we throw enough rays into the scene, most will disappear into the background, but enough will hit lights to give us a rendering.
Path tracing and Photon maps
Obviously, in a room with a light bulb in it, surfaces in the room are directly illuminated, and rays from our eye position intersect those surfaces. In effect, the directly-illuminated walls become light sources for other parts of the environment. We can't trace the light from the lights all the way to our eyes because there's an infinitude of rays. But we might take a statistical approach to this too. It takes two steps.
Step 1: Photon mapping
We could trace rays (called "photons" when going from light-sources into the scene) from the lights through the model, using BRDFs to calculate where they bounce and recording at each bounce how much light they brought to the surface. This database of light-surface impacts is stored. Its called a photon map.
Step 2: Ray tracing
Next, crank up the ray tracer, but with a small change. When a ray is traced to a surface, rather than simply bouncing, we look around in the neighborhood and collect info from the photon map about how much light arrived in the area from "elsewhere". The photon map essentially gives us an illuminated scene to trace. One really spiffy side-effect is that the photon-map can capture refractive light interactions with diffuse surfaces -- caustics!. It also captures diffuse inter-reflections and renders color bleed and indirect lighting.
Probability, photons, samples, and accuracy
The thing about probabalistic solutions is that they are never exact, they are always approximate, and the quality of the approximation depends on the number of samples. In this case, the light is distributed by "shooting rays" from the lights into the model to create our photon map. The number of rays shot from each light is proportional to the intensity of the light source, but the total number of rays will influence the quality of the rendering as well. It'll take longer too.
The ray tracing step involves "sampling" the scene. Again, more samples will improve the quality of the rendering, but will also take longer. Recall that rays that "escape" to the background generally don't count, so lots of research has gone into making each sample actually improve the image, and the description above glosses over much of this, which has to do with finding the important parts of the scene, like edges, near surfaces, etc.
It is not unusual to find references to 500 or even 5000 samples per pixel in rendering scenes. As a consequence, they take a while.
Last updated: April, 2014
