TAPESTRY: The Art of Representation and Abstraction
Derivative Geometry: Surfaces of Revolution
You Say you Want a Revolution?
A surface of revolution is a surface which has axial symmetry. That is, it has a simple cross-section or profile which defines the surface when it is revolved around some axis (moved along a circular path). One common example is shown in the profile at right which looks like a shallow bowl. By rotating this profile around the center axis (which better be a point ON the profile if you want a bowl without a hole in it!) and connecting the profiles to form polygons, we can generate a "surface of revolution"--a bowl such as the one shown at the top of the page.
Notice that the profile has both an inside and an outside? That avoids a problem in which the profile sweeps out single-sided polygons, which in turn are removed by the backside culling operation. Results of such a surface can be quite visually confusing: The following three figures show three renderings of the same data: (a) a correctly shaded bowl, (b) the "inside" polygons, and (c) the "outside" polygons.
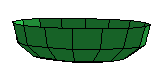 a. | 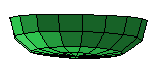 b. | 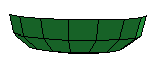 c. |
Form•Z actually makes it hard to make this mistake. Since the toplogy rules indicate that revolving an "open" shape (a profile that doesn't close on itself) cannot generate an enclosed volume, form•Z usually generates "surface solids" (two-sided shapes which are topologically solid, but lacking any interior volume). I turned this off in the revolution tool before generating the bowl. But even with one-sided data, the program provides an option (in the Display menu) to "Show Surfaces As Double Sided". This could be used with data imported from other programs to insure that items such as the bowl render appropriately. I turned if off to make figures (b) and (c) above.
The other tool that relates to this is the "Direction" editing tool (in row 7 of the tool palette). You can use this to reverse the direction in which single-sided polygons "face". That's the difference between figure (b) and (c) - I reversed the bowl between these two views.
You might ask why I would choose to make the bowl one-sided rather than providing a complete profile such as the one initially shown. Simple--it uses fewer polygons. We will see other techniques for making shapes look smoothly curved or for adding details. By and large, use the smallest number of polygons you can — always!
Last updated: April, 2014
