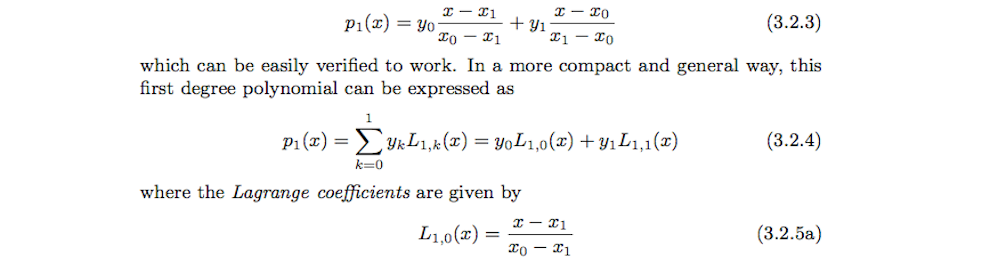Basic Regression and Optimization Algorithms
LOADING
-
Least-Square Fitting Procedure
-
Different Interpolation Algorithms for Curve Fitting
-
Gradient Descent for Optimization
-
Efficient Polynomial Fitting via Lagrange Coefficients
-
Linear Programming and Feasibility Regions
About Curve Fitting and Optimization
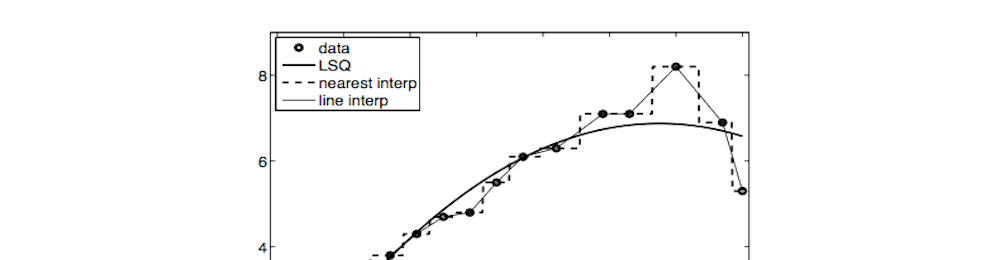
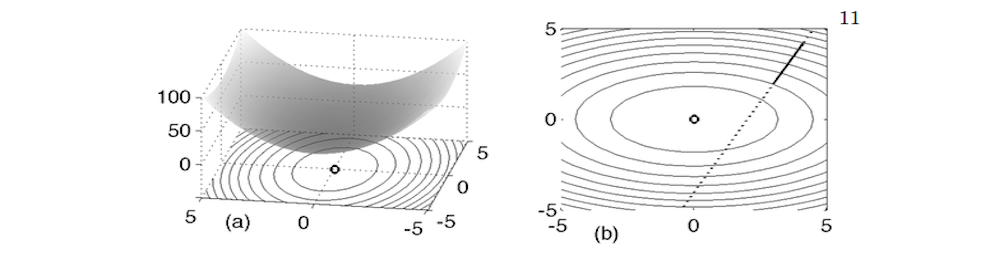
Analyzing data is fundamental to any aspect of science. Often data can be noisy in nature and only the trends in the data are sought. A variety of curve fitting schemes can be generated to provide simplified descriptions of data and its behavior. The least-squares fit method is explored along with fitting methods of polynomial fits and splines. Optimization methods are prevalent throughout a vast range of applications. In its simplest form, an optimization routine simply attempts to find the maximum or minimum of a real valued function, i.e. the objective function, by developing an algorithm that systematically chooses input values from a allowed set, or feasible set, and computes the value of the function. Typically, the optimization algorithm is built upon an iteration scheme that continues to choose new input values so that the maximum or minimum of the objective function is achieved. The generalization of optimization theory and techniques to other formulations comprises a large area of applied mathematics. More generally, optimization includes finding best available values of some objective function given a defined domain, including a variety of different types of objective functions and different types of domains. In the following sections, a brief introduction to these techniques will be given along with their MATLAB function calls.