Fast Fourier Transform
LOADING
About Fourier Transforms
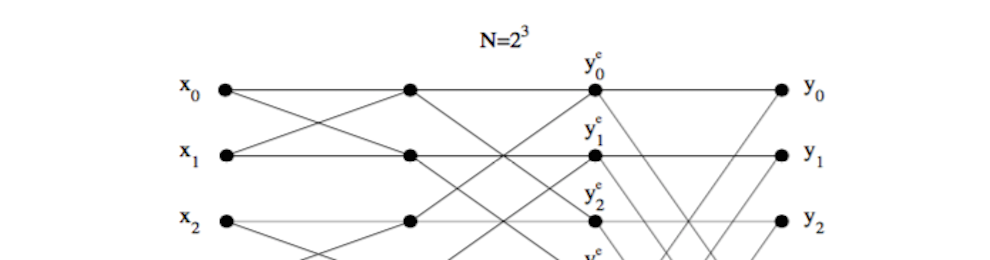
Spectral methods are one of the most powerful solution techniques for ordinary and partial differential equations. The best known example of a spectral method is the Fourier transform, which represents spatial or temporal data with frequency content. The Fast Fourier transform routine was developed specifically to perform the forward and backward Fourier transforms. In the mid 1960s, Cooley and Tukey developed what is now commonly known as the FFT algorithm. Their algorithm was named one of the top ten algorithms of the 20th century for one reason: the operation count for solving a system dropped to O(NlogN). For N large, this operation count grows almost linearly like N. Thus it represents a great leap forward from Gaussian elimination and LU decomposition. Its interpretation as a frequency representation also has led to major innovations in a wide variety of fields and applications.