TAPESTRY: The Art of Representation and Abstraction
Hidden Lines and Surfaces
What's it all about?
Given a set of polygons, such as the six squares which form the boundary of a cube, it is clear that we never see the polygons which are on the "far side" of the cube, facing away from us. The real reason we don't see them is that there are other polygons (on the front side of the cube) that get in the way, but the whole process is easier if we can provide really simple answers. In this case, if we could identify those polygons that "face away from us" and simply not draw them, we would (for cubes, anyway!) have a perfect solution.
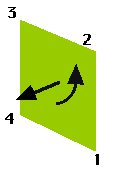Let's look at one face of a cube for a minute, as shown at right.
It turns out that the vertexes of the polygon boundary can be used to define the surface normal (a vector perpendicular to the surface at a given point). Using the right hand rule (curl the fingers of your right hand around the center of the polygon, pointing them in the direction in which the vertexes are listed--your thumb points towards the "outside" of the surface) (and "out of the screen").
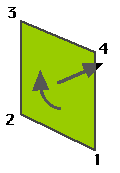Take the same polygon, but reverse the order of the vertexes and you get the situation shown at left. Use the same right hand rule to see if you are convinced that in this case the surface normal is pointing "into" the screen.
Notice that it doesn't matter where we start on the face, it is the order of the vertexes, or nodes, which matters.
This ordering is sometimes called the winding order and most modeling programs provide a mechanism for "reversing the winding order" or "reversing the direction" of a polygon. See if you can find such a command in your favorite modeller.
How CULLING Works
The algorithm can be implemented several different ways, but basically the program calculates the surface normal from the vertex list for a given polygon, and then tests the normal to see if it points towards or away from the viewer. If it points towards the viewer the polygon is processed further. If it points away from the viewer, the polygon is discarded and the program moves to the next polygon in the data.
How CULLING Fails
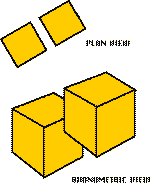Unfortunately, culling is only completely accurate for convex data sets. That is, it's only right when there are no points on the outside of the surface where you could see another portion of the surface. This is true of the cube, it is true of individual spheres, etc. However, it is not true of TWO cubes (as shown here), or a bowl, or of almost any other realistic collection of polygons.
Notice that in these cases culling doesn't introduce errors, it simply isn't sufficient to the entire task. For this reason culling is often used as a part of a more complex rendering pipeline because it can dramatically reduce the amount of work that the rest of the pipeline has to do.
Culling should not be used with "one sided" data, such as that produced by revolving an open profile in space (see illustration at left). Such an operation (unless treated specially by the modeling program) generates an open form, with polygons facing all directions. When culled, some parts of the bowl will disappear. The top image shows what the bowl should look like, while the two images below it illustrate how it will appear after culling, depending on whether the surface normals are generated pointing to the inside of the bowl or towards the outside.
Last updated: April, 2014
