Chapter 22 ANOVA is just regression
You’ll hear the title of this chapter from certain statistics instructors and fans of linear regression. Sometimes ANOVA is taught completely in the context of linear regression, and not in the traditional way like we have in this book of ratios of mean squares and F distributions. I think the main difference between the two methods of understanding and teaching ANOVA is cultural; the traditional way emphasizes statistical significance in the differences of the means, and the regression way emphasizes how those means are calculated.
In any case, I’ve found a good description of why “ANOVA is just regression” lacking. So this is my best shot at it.
22.1 3 Equations and 3 Unknowns
First we’ll start with a crash course on linear regression. We begin with basic matrix multiplication. For example, here’s how you compute the product of a 3x3 matrix with a 3x1 column vector. We’ll call the 3x3 matrix \(A\), and the 3x1 column vector \(x\) and the product \(y\). This is how to multiply \(A\) times \(x\) to get \(y\):
\(A\) \(x\) \(y\)
\[ \begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 0 \\ 1 \\ 2 \end{bmatrix} = \begin{bmatrix} (1)(0) + (1)(1) + (1)(2) \\ (1)(0) + (2)(1) + (3)(2) \\ (1)(0) + (0)(1) + (1)(2) \end{bmatrix} = \begin{bmatrix} 3 \\ 8 \\ 2 \end{bmatrix} \]
If it has been a while, take a look at how this works. When multiplying a matrix times a vector we perform dot products across the rows of the matrix \(A\) with the column of vector \(x\).
Another way to think about it is that the product of \(A\) and \(x\) is equal to the sum of the columns of \(A\) scaled by the values in the vector \(x\). In this example, the result is 0 times the first column plus 1 times the second column plus 2 times the third column of \(A\). In other words the product of matrix \(A\) and a column vector \(x\) is a linear combination of the columns of A weighted by the values in \(x\).
Suppose that you know the values in the matrix \(A\) and the answer \(y\), but not the values in the vector \(x\). If this were algebra with numbers, we’d just solve for \(x\) by dividing both sides of the equation by \(A\). That is, if
\[Ax = y\] then \[x = \frac{y}{A}\]
But since \(A\) is a matrix, instead of dividing by A we compute the inverse of \(A\) which we then multiply on both sides of the equation \(Ax = y\). The inverse of A, written as \(A^{-1}\) is the matrix for which \(A^{-1}A = I\), where \(I\) is the identity matrix (a matrix with all zeros with 1’s along the diagonal). Remember, \(I\) has as the property that \(Ix = x\).
Multiplying \(A^{-1}\) on both sides of \(Ax = y\) gives:
\[A^{-1}Ax = A^{-1}y\]
\[Ix = A^{-1}y\]
\[x = A^{-1}y\]
For our example, the inverse of A is:
\(A^{-1}\)
\[ \begin{bmatrix} 1 & -0.5 & 0.5 \\ 1 & 0 & -1 \\ -1 & 0.5 & 0.5 \end{bmatrix} \]
You can verify that \(A^{-1}A = I\):
\(A^{-1}\) \(A\) \(I\)
\[ \begin{bmatrix} 1 & -0.5 & 0.5 \\ 1 & 0 & -1 \\ -1 & 0.5 & 0.5 \end{bmatrix} \times \begin{bmatrix} 1 & 1 & 1 \\ 1 & 2 & 3 \\ 1 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
So, if we multiply \(A^{-1}\) by \(y\) we get our original value of \(x\):
\(A^{-1}\) \(y\) \(x\)
\[ \begin{bmatrix} 1 & -0.5 & 0.5 \\ 1 & 0 & -1 \\ -1 & 0.5 & 0.5 \end{bmatrix} \times \begin{bmatrix} 3 \\ 8 \\ 2 \end{bmatrix} = \begin{bmatrix} (1)(3) + (-0.5)(8) + (0.5)(2) \\ (1)(3) + (0)(8) + (-1)(2) \\ (-1)(3) + (0.5)(8) + (0.5)(2) \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ 2 \end{bmatrix} \] This shows that you can use \(A^{-1}\) to solve \(Ax = y\) for \(x\).
Where did \(A^{-1}\) come from? You may have computed a matrix inverse in the past using methods like the Gauss-Jordan method or through numerical methods, which is how your computer does it.
22.2 5 Equations and 2 Unknowns
Now consider the case where A is not square, but has more rows than columns. For example, consider this equation for \(Ax = y\):
\(A\) \(x\) \(y\)
\[ \begin{bmatrix} 1 & 0 \\ 2 & 1 \\ 3 & 0 \\ 4 & 1 \\ 5 & 0 \end{bmatrix} \times \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} 0.5 \\ 0.5 \\ 1.5 \\ 1.4 \\ 2.5 \end{bmatrix} \]
To find the values \(x_{1}\) and \(x_{2}\) we need to satisfy 5 equations with only 2 unknowns. This is an overconstrained set of equations and may not have an exact solution. Indeed, for this example there is no set of values \(x_{1}\) and \(x_{2}\) that satisfy this equation.
The best we can do is find values of \(\hat{x}_{1}\) and \(\hat{x}_{2}\) so that the product \(A\hat{x}\) is close to the correct answer (we pronounce \(\hat{x}\) as ‘x-hat’). By close, we mean the answer that minimizes the sums of squared difference between \(A\hat{x} = \hat{y}\) and \(y\). This is called the least squares solution to the problem. The process of finding these best values is called linear regression.
Matrix notation is really just shorthand for writing out systems of equations. For this example, linear regression is the process of finding the values of \(\hat{x_1}\) and \(\hat{x_2}\) that make the following sum as small as possible:
\((1\hat{x_1} + 0\hat{x_2} - 0.5)^2\) + \((2\hat{x_1} + 1\hat{x_2} - 0.5)^2\) + \((3\hat{x_1} + 0\hat{x_2} - 1.5)^2\) + \((4\hat{x_1} + 1\hat{x_2} - 1.4)^2\) + \((5\hat{x_1} + 0\hat{x_2} - 2.5)^2\)
In the first example, when A was a 3x3 matrix, we solved the equation by computing the inverse of A, \(A^{-1}\). In this second example A is not a square matrix, so it doesn’t have an inverse. Instead, there’s something called a pseudoinverse (sometimes called the Moore-Penrose generalized inverse) that can be used to find the least squared solution. Like the real inverse, the pseudoinverse, denoted as \(A^{+}\), also has the property that \(A^{+}A = I\).
\(A^{+}\) is calculated by:
\[A^{+} = (A^{T}A)^{-1}A^{T}\]
where \(A^{T}\) is the transpose of A (the matrix A with rows and columns switched).
Calculating \(A^{+}\) would be a nightmare by hand, but there are algorithms that allow computers to find it. For our example,
\(A^{+}\) is:
\(A^{+}\)
\[ \begin{bmatrix} 0.027 & -0.027 & 0.0811 & 0.027 & 0.1351 \\ -0.0811 & 0.5811 & -0.2432 & 0.4189 & -0.4054 \end{bmatrix} \]
Analogous to what we did when A was square, can use the pseudoinverse of A to find the least squared solution, \(\hat{x}\), by multiplying \(A^{+}\) on the left side both sides of the equation \(A\hat{x} = y\):
\[A^{+}A\hat{x} = A^{+}y\]
Since \(A^{+}A = I\),
\[\hat{x} = A^{+}y\]
For our example:
\[ \begin{bmatrix} 0.027 & -0.027 & 0.0811 & 0.027 & 0.1351 \\ -0.0811 & 0.5811 & -0.2432 & 0.4189 & -0.4054 \end{bmatrix} \times \begin{bmatrix} 0.5 \\ 0.5 \\ 1.5 \\ 1.4 \\ 2.5 \end{bmatrix} = \begin{bmatrix} 0.4973 \\ -0.5419 \end{bmatrix} \]
So, if \(\hat{x}_{1} = 0.4973\) and \(\hat{x}_{2} = -0.5419\), then the product \(A\hat{x}\) gives us a vector, which we call \(\hat{y}\), that is as close to y (in terms of least squares) as possible. For our example, \(A\hat{x}=\hat{y}\):
\(A\) \(\hat{x}\) \(\hat{y}\)
\[ \begin{bmatrix} 1 & 0 \\ 2 & 1 \\ 3 & 0 \\ 4 & 1 \\ 5 & 0 \end{bmatrix} \times \begin{bmatrix} 0.4973 \\ -0.5419 \end{bmatrix} = \begin{bmatrix} 0.4973 \\ 0.4527 \\ 1.4919 \\ 1.4473 \\ 2.4865 \end{bmatrix} \]
Notice that the values in \(\hat{y}\) are pretty close to the desired values of y:
\(y\)
\[ \begin{bmatrix} 0.5 \\ 0.5 \\ 1.5 \\ 1.4 \\ 2.5 \end{bmatrix} \]
How close? In statistics we like to measure differences as sums of squared deviations. The sums of squared difference between \(y\) and \(\hat{y}\) is:
\[(0.5-0.4973)^{2} + (0.5-0.4527)^{2} + ... + (2.5-2.4865)^{2} = 0.00473\]
You can search as long and hard as you want, but you won’t find a better pair of values than \(x_{1} = 0.4973\) and \(x_{2} = -0.5419\) that will give you an answer that gives you a smaller sums of squared deviation than \(0.00473\).
If you think of the matrix multiplication in \(Ax\) as computing a linear combination of the columns of \(A\) weighted by \(x\), then linear regression is finding the ‘weights’ needed for each column of \(A\) that gives us an answer that is closest to \(y\). Each column of \(A\) is called a regressor, and the values of \(x\) that give you the least-squares solution are called the regression coeficients (sometimes called beta weights for some reason, though the term beta weight should only be used for ‘standardized’ linear regression).
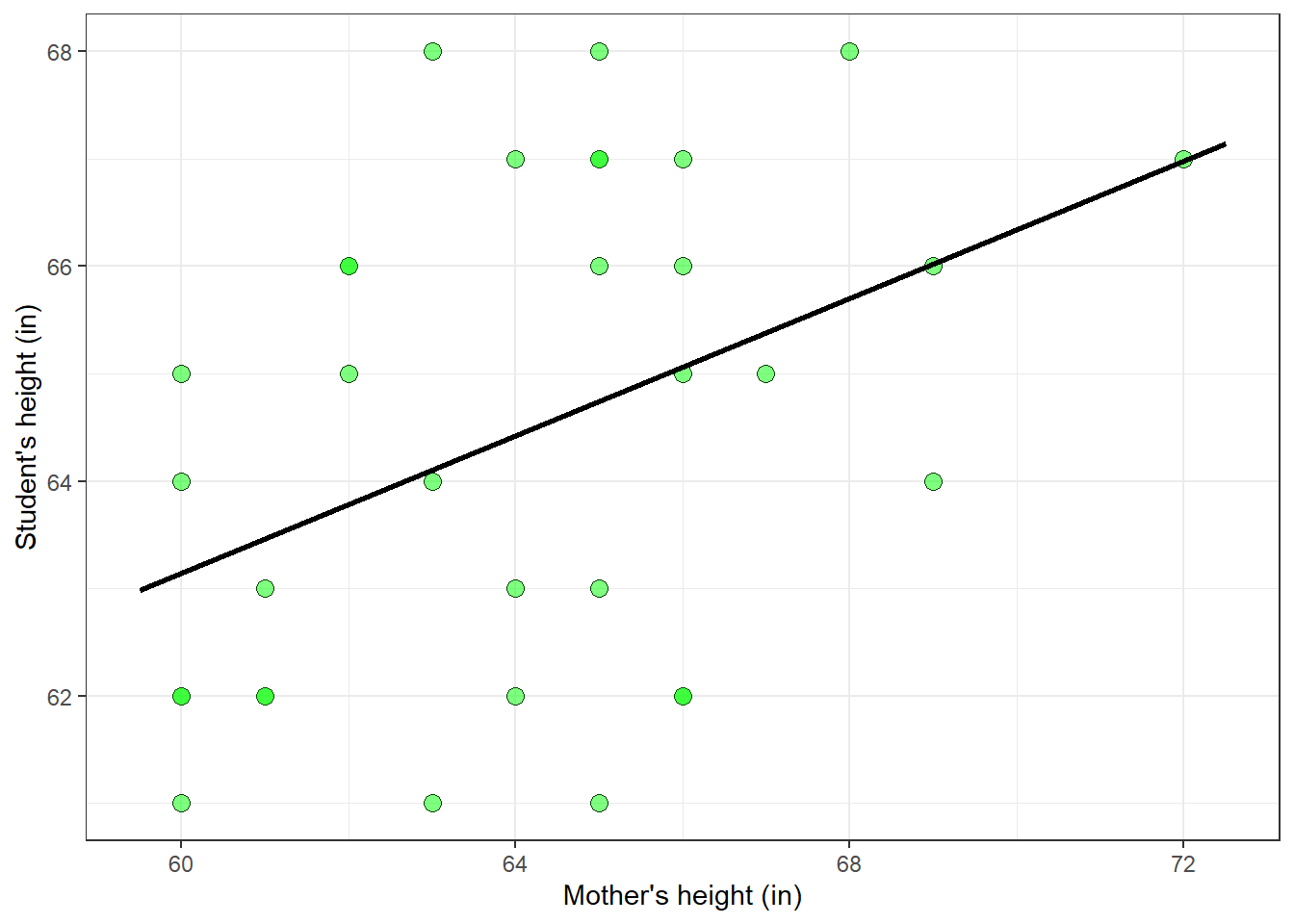
22.3 Predicting student’s heights from mother’s heights
When we think of linear regression we often think of fitting straight lines to a scatterplot like we did in the last chapter on correlation and regression. We’ll go through a similar example from that chapter on the heights of women and their mothers, but in the context of linear algebra and the pseudoinverse described above. From the survey, I’ve chosen women in the class that were born in 1999 to keep the sample size smallish.
Here’s some standard R code to pull out the student’s heights into student and mother’s heights into mother:
survey <-
read.csv("http://www.courses.washington.edu/psy315/datasets/Psych315W21survey.csv")
survey$mheight <- as.numeric(survey$mheight)
id <- survey$year == "1999" & survey$gender== "Woman" &
!is.na(survey$height) & !is.na(survey$mheight) & !is.na(survey$year)
student <- survey$height[id]
mother <- survey$mheight[id]Here’s a table of their heights:
| student | mother |
|---|---|
| 66 | 62 |
| 62 | 60 |
| 67 | 65 |
| 62 | 66 |
| 62 | 60 |
| 62 | 64 |
| 64 | 63 |
| 61 | 65 |
| 62 | 61 |
| 61 | 60 |
| 63 | 61 |
| 62 | 66 |
| 62 | 61 |
| 67 | 66 |
| 66 | 62 |
| 68 | 68 |
| 65 | 60 |
| 64 | 69 |
| 66 | 66 |
| 65 | 66 |
| 67 | 72 |
| 61 | 63 |
| 68 | 63 |
| 64 | 60 |
| 67 | 64 |
| 67 | 65 |
| 65 | 62 |
| 68 | 65 |
| 63 | 65 |
| 66 | 69 |
| 65 | 67 |
| 66 | 65 |
| 63 | 64 |
Suppose you want to come up with a model that predicts each student’s height based on their mother’s height. A simple model would be a linear model like this:
\[student = x_{1} + x_{2}*mother\]
Where \(x_{1}\) and \(x_{2}\) are constants, or ‘free parameters’.
We can write this linear model as a matrix multiplication like this:
\(A\) \(x\) \(student\)
\[ \begin{bmatrix} 1 & 62 \\ 1 & 60 \\ 1 & 65 \\ 1 & 66 \\ 1 & 60 \\ 1 & 64 \\ 1 & 63 \\ 1 & 65 \\ 1 & 61 \\ 1 & 60 \\ 1 & 61 \\ 1 & 66 \\ 1 & 61 \\ 1 & 66 \\ 1 & 62 \\ 1 & 68 \\ 1 & 60 \\ 1 & 69 \\ 1 & 66 \\ 1 & 66 \\ 1 & 72 \\ 1 & 63 \\ 1 & 63 \\ 1 & 60 \\ 1 & 64 \\ 1 & 65 \\ 1 & 62 \\ 1 & 65 \\ 1 & 65 \\ 1 & 69 \\ 1 & 67 \\ 1 & 65 \\ 1 & 64 \end{bmatrix} \times \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} = \begin{bmatrix} 66 \\ 62 \\ 67 \\ 62 \\ 62 \\ 62 \\ 64 \\ 61 \\ 62 \\ 61 \\ 63 \\ 62 \\ 62 \\ 67 \\ 66 \\ 68 \\ 65 \\ 64 \\ 66 \\ 65 \\ 67 \\ 61 \\ 68 \\ 64 \\ 67 \\ 67 \\ 65 \\ 68 \\ 63 \\ 66 \\ 65 \\ 66 \\ 63 \end{bmatrix} \]
Here the first column of A is all 1’s and the second column contains mother’s heights. See how this matrix multiplication performs the calculation in the linear model. For each student,
\[x_{1} + mother \times x_{2} =student\]
Notice how this is a set of 33 (# of students) and 2 unknowns. We can use linear regression to find the values of \(x_{1}\) and \(x_{2}\) that minimize the sum of squares between the predicted heights and real student heights.
We can do this with the pseudoinverse, \(A^{+}\), like we did before and then calculating \(\hat{x} = (A^{+})(mother)\). If you get your computer to do this you get these regression weights:
\(\hat{x}\)
\[ \begin{bmatrix} 43.9715 \\ 0.3196 \end{bmatrix} \]
The equation that best predicts student heights is therefore: \(student = 43.9715 + 0.3196 \times mother\)
With this best fit we can generate the predicted student heights, \(\hat{y}\) by multiplying A by \(\hat{x}\):
\(A\) \(\hat{x}\) \(\hat{y}\)
\[ \begin{bmatrix} 1 & 62 \\ 1 & 60 \\ 1 & 65 \\ 1 & 66 \\ 1 & 60 \\ 1 & 64 \\ 1 & 63 \\ 1 & 65 \\ 1 & 61 \\ 1 & 60 \\ 1 & 61 \\ 1 & 66 \\ 1 & 61 \\ 1 & 66 \\ 1 & 62 \\ 1 & 68 \\ 1 & 60 \\ 1 & 69 \\ 1 & 66 \\ 1 & 66 \\ 1 & 72 \\ 1 & 63 \\ 1 & 63 \\ 1 & 60 \\ 1 & 64 \\ 1 & 65 \\ 1 & 62 \\ 1 & 65 \\ 1 & 65 \\ 1 & 69 \\ 1 & 67 \\ 1 & 65 \\ 1 & 64 \end{bmatrix} \times \begin{bmatrix} 43.9715 \\ 0.3196 \end{bmatrix} = \begin{bmatrix} 63.7863 \\ 63.1471 \\ 64.7451 \\ 65.0647 \\ 63.1471 \\ 64.4255 \\ 64.1059 \\ 64.7451 \\ 63.4667 \\ 63.1471 \\ 63.4667 \\ 65.0647 \\ 63.4667 \\ 65.0647 \\ 63.7863 \\ 65.7039 \\ 63.1471 \\ 66.0235 \\ 65.0647 \\ 65.0647 \\ 66.9822 \\ 64.1059 \\ 64.1059 \\ 63.1471 \\ 64.4255 \\ 64.7451 \\ 63.7863 \\ 64.7451 \\ 64.7451 \\ 66.0235 \\ 65.3843 \\ 64.7451 \\ 64.4255 \end{bmatrix} \]
The sums of squared deviation between the student’s heights and predicted student’s heights is
\[(66-63.7863)^{2} + (62-63.1471)^{2} + ... + (63-64.4255)^{2} = 0.0047297\]
You’ll recognize that our model is simply the equation of a line. Given a scatterplot with mother’s heights on the x-axis and student height on the y-axis, solving for the regression weights finds the best-fitting line to the data in the scatterplot.
22.4 Statistical significance of adding regressors
Solving a linear regression problem will always give us a least-squares solution, even if the fit isn’t very good. How can we evaluate the goodness of fit? More specifically, how can we determine if we need all of the regressors to predict the data?
One way to think about the fit of our regression line is to ask if if we really need a slope to predict the student’s heights. Or in hypothesis test terms, is the slope significantly different from zero?
Let’s see how well we can predict the student’s heights with a simpler model that doesn’t have a regressor for the slope. This is just finding the least square solution for \(Ax=y\) where \(A\) is just a column of ones:
\(A\) \(x\) \(student\)
\[ \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \times \begin{bmatrix} x_{1} \end{bmatrix} = \begin{bmatrix} 66 \\ 62 \\ 67 \\ 62 \\ 62 \\ 62 \\ 64 \\ 61 \\ 62 \\ 61 \\ 63 \\ 62 \\ 62 \\ 67 \\ 66 \\ 68 \\ 65 \\ 64 \\ 66 \\ 65 \\ 67 \\ 61 \\ 68 \\ 64 \\ 67 \\ 67 \\ 65 \\ 68 \\ 63 \\ 66 \\ 65 \\ 66 \\ 63 \end{bmatrix} \]
The least-square solution to this is \(x_{1}\) = 64.4545.
\[(66-64.4545)^{2} + (62-64.4545)^{2} + ... + (63-64.4545)^{2} = 168.1818\]
Compare this to the sums of squared deviation for the regression with the slope: \(138.8954\).
The regression equation with the slope has a smaller sums of squared deviation. Does that mean it’s a better predictor of the student’s heights? Not necessarily. Adding regressors will always improve the fit, since the equation with the slope is a more flexible version of the equation without the slope. We call these two regression equations nested, with one a more general version of the other.
Since adding regressors always improves the fit, we need a hypothesis test to determine if the additional regressor improves the fit enough to justify it. This can be done by computing an F statistic and the corresponding p-value.
We define the model with more regressors as the ‘complete’ model,and the model with fewer regressors as the ‘restricted’ model. For our example, the complete model is the one with both an intercept and a slope, and the restricted model has just the one constant. The sums of squared deviation for the least-square fit for the two models are defined as \(SS_{r}\) and \(SS_{c}\) for the restricted and complete models respectively. For this example,
\[SS_{r} = 168.1818\]
and
\[SS_{c} = 138.8954\]
Let \(n\) be the total number of data points (\(n = 33\) students in our example), \(k_{r}\) be the number of regressors in the restricted model (\(k_{r}= 1\), the mean) and \(k_{c}\) be the number of regressors in the complete model (\(k_{c} = 2\), intercept and slope).
The F-statistic is computed as:
\[F = \frac{(SS_{r}-SS_{c})/(k_{c}-k_{r})}{SS_{c}/(n-k_{c})}\] With \(k_{c}-k_{r}\) degrees of freedom for the numerator and \(n-k_{c}\) degrees of freedom for the denominator.
For our example,
\[F = \frac{(168.1818-138.8954)/(2-1)}{138.8954/(33-2)}= 6.5364\]
The p-value for this value of F, with 1 and 31 degrees of freedom is:
## [1] 0.01568644A small p-value indicates that adding the slope regressor significantly improves the fit of the linear regression model to the data. In other words, if \(p\) is small, then the slope is significantly different from zero, because if the slope is zero we have the restricted model.
If we use our favorite criterion value of \(\alpha = 0.05\), we conclude that adding the slope regressor does significantly improve the fit. We therefore conclude that the slope is significantly different from zero. If we assume causality, it means that there is a significant influence of the mother’s height on the student’s height.
Recall that in the previous chapter we showed that if you use R’s cor.test function to run a two-tailed test on the null hypothesis that the correlation in the population between student and mother’s heights is zero you’ll get the same p-value.
22.5 ANOVA as regression
We’re ready to talk about ANOVA. We’ll first show that given a 1-factor ANOVA data set you can calculate group means using linear regression. Consider the following data set which are UW GPA’s for the men in the class grouped by whether they prefer to sit in the front, middle, or the back of the lecture hall. We can use a 1-factor ANOVA to determine if the means of each group are significantly different from each other.
| Near the front | In the middle | Toward the back |
|---|---|---|
| 3.66 | 3.23 | 3.30 |
| 3.84 | 3.65 | 3.68 |
| 3.95 | 3.80 | 3.83 |
| 3.90 | 2.60 | |
| 3.43 | 3.80 | |
| 3.85 | 2.00 | |
| 3.00 | 2.89 | |
| 3.35 | 4.00 | |
| 3.31 | 3.66 | |
| 3.91 | 3.51 | |
| 3.07 | ||
| 3.53 | ||
| 3.20 | ||
| 3.30 | ||
| 3.65 |
Here are the summary statistics showing the group means, \(SS_{within}\) for each of the 3 groups:
| mean | n | sd | sem | |
|---|---|---|---|---|
| Near the front | 3.8167 | 3 | 0.1464 | 0.0845 |
| In the middle | 3.4787 | 15 | 0.3025 | 0.0781 |
| Toward the back | 3.3270 | 10 | 0.6394 | 0.2022 |
And here’s the result of the ‘omnibus’ F test:
| df | SS | MS | F | p | |
|---|---|---|---|---|---|
| Between | 2 | 0.5637 | 0.2819 | 1.4083 | p = 0.2633 |
| Within | 25 | 5.0037 | 0.2001 | ||
| Total | 27 | 5.5674 |
The p-value for this hypothesis test is 0.2633, so using our magic value of \(\alpha=0.05\), it seems that GPA does not vary with where these students prefer to sit in class.
Just in case you’re wondering, if we had included the whole class of 150, there is a significant difference in GPA at UW across where they like to sit.
Next we’ll use regression to estimate the 3 means. Here we’ll write a new equation \(Ax=y\) where \(y\) is a column vector containing all of the GPA’s. For this example, the first 3 values in \(y\) contain the GPAs in the ‘Near the front’ group. The second 15 values are GPA’s from the second group and so on. We’ll generate a funny looking matrix for A which contain zeros and ones like this:
\(A\) \(x\) \(y\)
\[ \begin{bmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix} = \begin{bmatrix} 3.66 \\ 3.84 \\ 3.95 \\ 3.23 \\ 3.65 \\ 3.8 \\ 3.9 \\ 3.43 \\ 3.85 \\ 3 \\ 3.35 \\ 3.31 \\ 3.91 \\ 3.07 \\ 3.53 \\ 3.2 \\ 3.3 \\ 3.65 \\ 3.3 \\ 3.68 \\ 3.83 \\ 2.6 \\ 3.8 \\ 2 \\ 2.89 \\ 4 \\ 3.66 \\ 3.51 \end{bmatrix} \]
Think about what happens when \(A\) is multiplied by \(x\) to predict \(y\). Notice that the first 3 predicted values are all equal to \(x_{1}\): (\(1x_1 + 0x_2 + 0x_2\)). What single value of \(x_{1}\) is closest, in the least-squares sense, to all of the first 3 GPA’s? It’s the mean of those 3 GPA’s from the ‘Near the front’ group. Similarly, the best-fitting value of \(x_{2}\) will be the mean of the ‘In the middle’ group and \(x_{3}\) will be the mean of the ‘Toward the back’ group. Sure enough, if we use the pseudoinverse to calculate the regression weights, we get our three group means:
\(\hat{x}\)
\[ \begin{bmatrix} 3.8167 \\ 3.4787 \\ 3.327 \end{bmatrix} \]
The predicted GPA’s based on these regression weights are just multiple copies of the group means:
\(A\) \(\hat{x}\) \(\hat{y}\)
\[ \begin{bmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \\ 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 3.8167 \\ 3.4787 \\ 3.327 \end{bmatrix} = \begin{bmatrix} 3.8167 \\ 3.8167 \\ 3.8167 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.4787 \\ 3.327 \\ 3.327 \\ 3.327 \\ 3.327 \\ 3.327 \\ 3.327 \\ 3.327 \\ 3.327 \\ 3.327 \\ 3.327 \end{bmatrix} \] The sums of squared deviations from \(\hat{y}\) and \(y\) is 5.0036. Can you find this number in the ANOVA table above? It’s the same as \(SS_{within}\). That’s because \(SS_{within}\) is the sums of squared deviation of each GPA from the mean of each group.
So far, this is just a complicated way of calculated the group means. What about the statistical significance of the test? The trick is to think of this regression model as the ‘complete’ model, which has a regressor for each group mean.
We can compare the fit to this model to a ‘restricted’ model that does not allow for a different mean for each group. Instead, we’ll try to predict our GPA’s from just one mean. Here’s the restricted model:
\(A\) \(x\) \(y\)
\[ \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} \times \begin{bmatrix} x_{1} \end{bmatrix} = \begin{bmatrix} 3.66 \\ 3.84 \\ 3.95 \\ 3.23 \\ 3.65 \\ 3.8 \\ 3.9 \\ 3.43 \\ 3.85 \\ 3 \\ 3.35 \\ 3.31 \\ 3.91 \\ 3.07 \\ 3.53 \\ 3.2 \\ 3.3 \\ 3.65 \\ 3.3 \\ 3.68 \\ 3.83 \\ 2.6 \\ 3.8 \\ 2 \\ 2.89 \\ 4 \\ 3.66 \\ 3.51 \end{bmatrix} \]
Here’s the least-squared solution:
\(\hat{x}\)
\[ \begin{bmatrix} 3.4607 \end{bmatrix} \]
Can you guess what this number 3.4607 is? It’s the grand mean.
The sums of squared deviation for this restricted model is 5.5674. Can you find this value in the ANOVA summary table? It’s \(SS_{total}\), which is the sums of squared deviation of all GPA’s from the grand mean.
You may have guessed where we’re going. A nested F-test will determine if the improvement of fit with the complete model justifies including a separate mean for each group. In other words, do we really need separate means to predict the data, or can we only conclude that the data came from a single population with a fixed mean?
For a nested F-test, the F-statistic is:
\[F = \frac{(SS_{r}-SS_{c})/(k_{c}-k_{r})}{SS_{c}/(n-k_{c})}\]
With \(k_{c}-k_{r}\) degrees of freedom for the numerator and \(k_{c}\) degrees of freedom for the denominator.
For this specific example, let’s define \(k\) to be the number of groups. We can replace the terms in the equations with:
\[SS_C = SS_{within}\]
\[SS_R = SS_{total}\]
\[k_{c} = k\]
\[k_{r} = 1\]
And, for this example,
\[SS_{r}-SS_{c} = SS_{total} - SS_{within}\]
Remember,
\[SS_{total} - SS_{within} = SS_{between}\]
So we can re-write the F-statistic as:
\[F = \frac{SS_{between}/(k-1)}{SS_{within}/(n-k)}\]
With \(k-1\) degrees of freedom for the numerator and \(n-k\) degrees of freedom for the denominator.
This is exactly the formula for computing the F statistic and degrees of freedom for the 1-factor ANOVA. So we get the same F-statistic as the original ANOVA analysis:
\[F = \frac{(5.5674-5.0036)/(3-1)}{5.0036/(28-3)} = \frac{0.5637/2}{5.0036/25} = \frac{0.2819}{0.2001} = 1.4083\]
Which, with 2 and 25 degrees of freedom gives us a p-value of 0.2633, the same as in the 1-factor ANOVA.
In terms of the nested model, we conclude that including separate regressors for each group to predict group means does not significantly improve the fit of the regression model over the restricted model that just has a single mean.
One caveat. For this example, our complete model is not really a more general version of the restricted model because it’s not the restricted model with added regressors (there is no column of 1’s in the complete model). However, you can run a different version of the complete model, where the first column is all ones, you get a general version of the restricted model that fits exactly as well:
\(A\) \(x\) \(y\)
\[ \begin{bmatrix} 1 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix} = \begin{bmatrix} 3.66 \\ 3.84 \\ 3.95 \\ 3.23 \\ 3.65 \\ 3.8 \\ 3.9 \\ 3.43 \\ 3.85 \\ 3 \\ 3.35 \\ 3.31 \\ 3.91 \\ 3.07 \\ 3.53 \\ 3.2 \\ 3.3 \\ 3.65 \\ 3.3 \\ 3.68 \\ 3.83 \\ 2.6 \\ 3.8 \\ 2 \\ 2.89 \\ 4 \\ 3.66 \\ 3.51 \end{bmatrix} \]
The regression weights for this complete model are:
\(\hat{x}\)
\[ \begin{bmatrix} 3.8167 \\ -0.338 \\ -0.4897 \end{bmatrix} \]
The sums of squared deviation for this regression is the same as for the previous complete model: 5.0036.
But what do these regression weights mean? The first weight, 3.8167 is still the mean for the first, ‘Near the front’, group of GPAs.
If you look at the matrix \(A\) you’ll see that the predicted GPA for the second group is the sum of the first two regression weights. So the predicted GPA for the second group is the mean for the first group plus \(\hat{x}_{2}\). Check that \(\hat{x}_{1} +\hat{x}_{2} = 3.8167-0.338 = 3.4787\), which is the mean for the second group. Similarly, \(\hat{x}_{1} +\hat{x}_{3} = 3.8167-0.4897 = 3.327\), which is the mean for the third group.
This new complete model has the same information in the regression weights, and since it’s a true generalization of the restricted model, it’s technically the one that should be used for the nested model F test. But since the SS and df’s are the same, it will give you the same F statistic as for the first, more intuitive, complete model that gave us the group means.
In summary, when someone tells you that ‘ANOVA is just regression’, you should now understand that you can use regression to find group means using a least squares to to \(Ax=y\) with a clever \(A\) matrix of zeroes and ones. This trick of using regressors consisting of zeros and ones to turn ANOVA into regression has many names, including ‘dummy variable’, ‘indicator variables’,‘design variable’,‘Boolean indicator’, ‘binary variable’, or ‘qualitative variable’.
Using a nested F-test to compare the goodness of fit of this complete model with the fit to restricted model provides the same measure of statistical significance as the traditional ANOVA. In fact, most software packages use this sort of dummy coding and regression to calculate F statistics for ANOVA. More complicated ANOVA tests, like main effects, interactions, simple effects, and random effects just require more complicated dummy variables that the computer figures out for you.
22.6 Effect Size
Here I’ll show you that \(\eta^{2}\), one of three measures of effect size for ANOVA, is the square of the correlation between the predicted and real data.
\(\eta^{2}\) is defined as:
\[\eta^{2} = \frac{SS_{between}}{SS_{total}}\]
which is the proportion of the total sums of squares that is associated with the differences between the means.
For our example:
\[\eta^{2} = \frac{SS_{between}}{SS_{total}} = \frac{0.5637}{5.5674} = 0.1013\]
There’s another interpretation of \(\eta^{2}\) with respect to regression. Here’s a scatterplot showing the real GPA’s on the x-axis and the predicted GPA’s from the complete model on the y-axis:
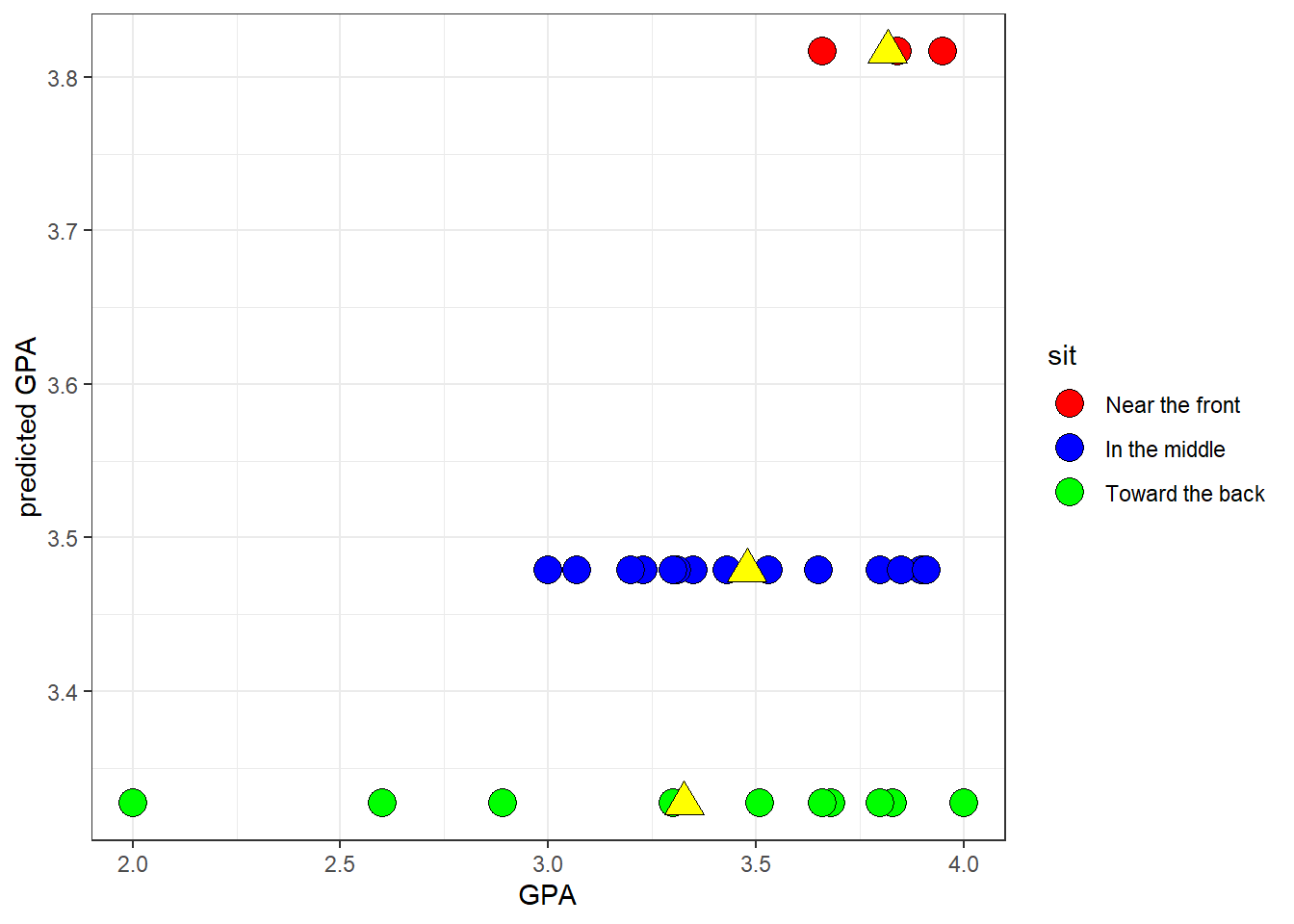
The scatterplot looks a little funny because there are only three levels of predicted GPA’s. That’s because, of course, the model predicts a specific GPA for each of the three levels of where students like to sit.
I’ve labeled the names of each group at the height of their means on the right side of the y-axis, and I’ve placed a yellow triangle at the location of the mean for each group.
The scatterplot lets you visualize each data point within each of the three groups. See how this scatterplot is a nice graphical representation of how the total variability of the points along the x-axis, \(SS_{total}\), is broken down into \(SS_{within}\) and \(SS_{between}\). \(SS_{within}\) is seen as the spread of points along the x-axis within each of the three groups (yellow triangles). \(SS_{between}\) is associated with the differences in the three means, which are the three values along the y-axis.
Consider the correlation between the real and predicted GPAs. If there were no variability between the means, all the predicted values would be the same on the y-axis and the correlation would be zero. On the other hand, if there was no variability within each group, then all GPA’s would be equal to the mean GPA for that group, so the points would all fall on a line defined by the three red boxes. The correlation would be equal to 1.
For this example, the correlation \(r = 0.3182\) and its square is \(r^{2} = 0.1013\).
Note that \(r^{2} = \eta^{2}\)
So another interpretation of the effect size measure, \(\eta^{2}\), is that it’s the square of the correlation between the predicted and real data. This is sometimes called the ‘proportion of the variance in X explained by Y’. In our case, the proportion of the variance in GPA’s explained by where students choose to sit is 0.1013.