20 Repeated Measures ANOVA
The repeated measures ANOA is an extension of the dependent (or repeated) measures t-test. The most common case for a one-factor repeated measures ANOVA is when each subject provides two or more measures.
You can find this test in the flow chart here:
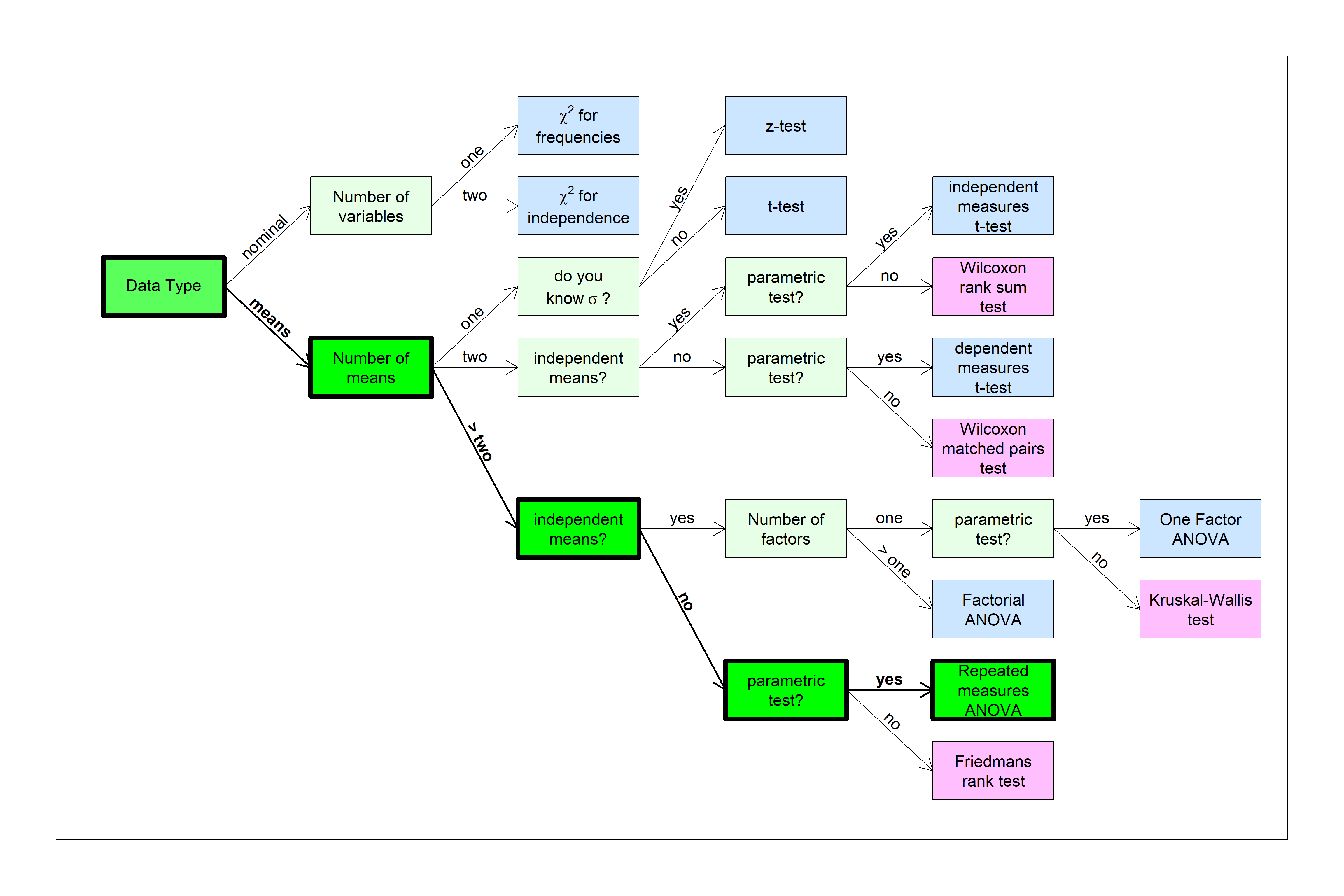
We’ll start with an example of a repeated measures t-test and build on that.
20.1 Review: Dependent measures t-test
Suppose you want to see if a specific exercise program affects body weight. You find 6 subjects and measure their weights (in kg) before the program and after three months. You can load in the (fake) data yourself in the course website:
data1 <- read.csv('http://courses.washington.edu/psy524a/datasets/SubjectExerciseANOVATtestdependent.csv')Some of these notes are based on the website (https://statistics.laerd.com/) which has some nice examples at the level appropriate for our class. The example in this chapter comes from (https://statistics.laerd.com/statistical-guides/repeated-measures-anova-statistical-guide-2.php)
To run a dependent t-test on these results we create a new column of differences and run a one-sample t-test on that column. Here’s a table of the results with the column of differences (after - before):
| Before | After Three Months | D |
|---|---|---|
| 45 | 50 | 5 |
| 42 | 42 | 0 |
| 36 | 41 | 5 |
| 39 | 35 | -4 |
| 51 | 55 | 4 |
| 44 | 49 | 5 |
Here’s how to run a dependent measures t-test on this data in R:
x <- data1$afterthreemonths
y <- data1$before
t.test.out <- t.test(x,y,paired = T,alternative = 'two.sided')
sprintf('t(%d) = %5.4f, p = %5.4f',t.test.out$parameter,t.test.out$statistic,t.test.out$p.value)## [1] "t(5) = 1.6425, p = 0.1614"20.2 Repeated measures with more than two levels
What if we want to measure each subject again after six months? This requires measuring the differences between means across three different groups. ANOVA!
Unfortunately, while a dependent measures t-test is easier to compute than an independent measures t-test, a dependent measures ANOVA (often called within subjects or repeated measures ANOVA) is actually a little more complicated than the standard independent measures ANOVA.
Here’s how to load in the new data set from the course website:
data2 <- read.csv('http://courses.washington.edu/psy524a/datasets/SubjectExerciseANOVAdependent.csv')This data is stored in ‘long format’, where each row in the table corresponds to a different observation as opposed to ‘wide format’ where each row corresponds to a subject.
With long format, the first column, ‘subject’, determines the subject for the observation. The second column ‘time’ determines the condition for that observation. You’ll see that each subject has three observations, consistent with the repeated measures design:
| Subject | Time | Weight |
|---|---|---|
| S1 | before | 45 |
| S1 | after three months | 50 |
| S1 | after six months | 55 |
| S2 | before | 42 |
| S2 | after three months | 42 |
| S2 | after six months | 45 |
| S3 | before | 36 |
| S3 | after three months | 41 |
| S3 | after six months | 43 |
| S4 | before | 39 |
| S4 | after three months | 35 |
| S4 | after six months | 40 |
| S5 | before | 51 |
| S5 | after three months | 55 |
| S5 | after six months | 59 |
| S6 | before | 44 |
| S6 | after three months | 49 |
| S6 | after six months | 56 |
Long format may seem inefficient, but it’s a very convenient way to store your results, especially for complicated experimental designs. This way, every time you acquire a new measurement, you just add a new row to your data with the fields determining exactly which condition/subject the data came from. Most of the functions in R are designed for long format. t.test is an exception since it takes in ‘x’ and ‘y’ variables, but t.test can also accept data in long format.
20.2.1 Converting long format to wide
Sometimes it’s useful to see your results in ‘wide’ format, where each row is a subject. This can be done with R using a variety of functions. Here’s how to convert to wide format with the reshape function. You have to tell it the subject variable idvar = "subject" and the independent variable timevar = "time":
The data in wide format looks like this:
| Subject | Before | After Three Months | After Six Months |
|---|---|---|---|
| S1 | 45 | 50 | 55 |
| S2 | 42 | 42 | 45 |
| S3 | 36 | 41 | 43 |
| S4 | 39 | 35 | 40 |
| S5 | 51 | 55 | 59 |
| S6 | 44 | 49 | 56 |
20.2.2 As an independent measures ANOVA
Let’s first pretend that this is an independent measures design and run the ANOVA that way, ignoring the ‘subject’ field. We’ll also pull out the SS’s, MS’, and df’s from the table
## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## time 2 143.44 71.722 1.5036 0.254
## Residuals 15 715.50 47.700SS_between <- anova.out.1$`Sum Sq`[1]
df_between <- anova.out.1$Df[1]
MS_between <- anova.out.1$`Mean Sq`[1]
SS_within <- anova.out.1$`Sum Sq`[2]
df_within <- anova.out.1$Df[2]
MS_within <- anova.out.1$`Mean Sq`[2]
SS_total = SS_between+SS_within # remember?Remember, for a 1-factor ANOVA like this breaks down the total sums of squares so that
\[SS_{total} = SS_{between} + SS_{within}\]
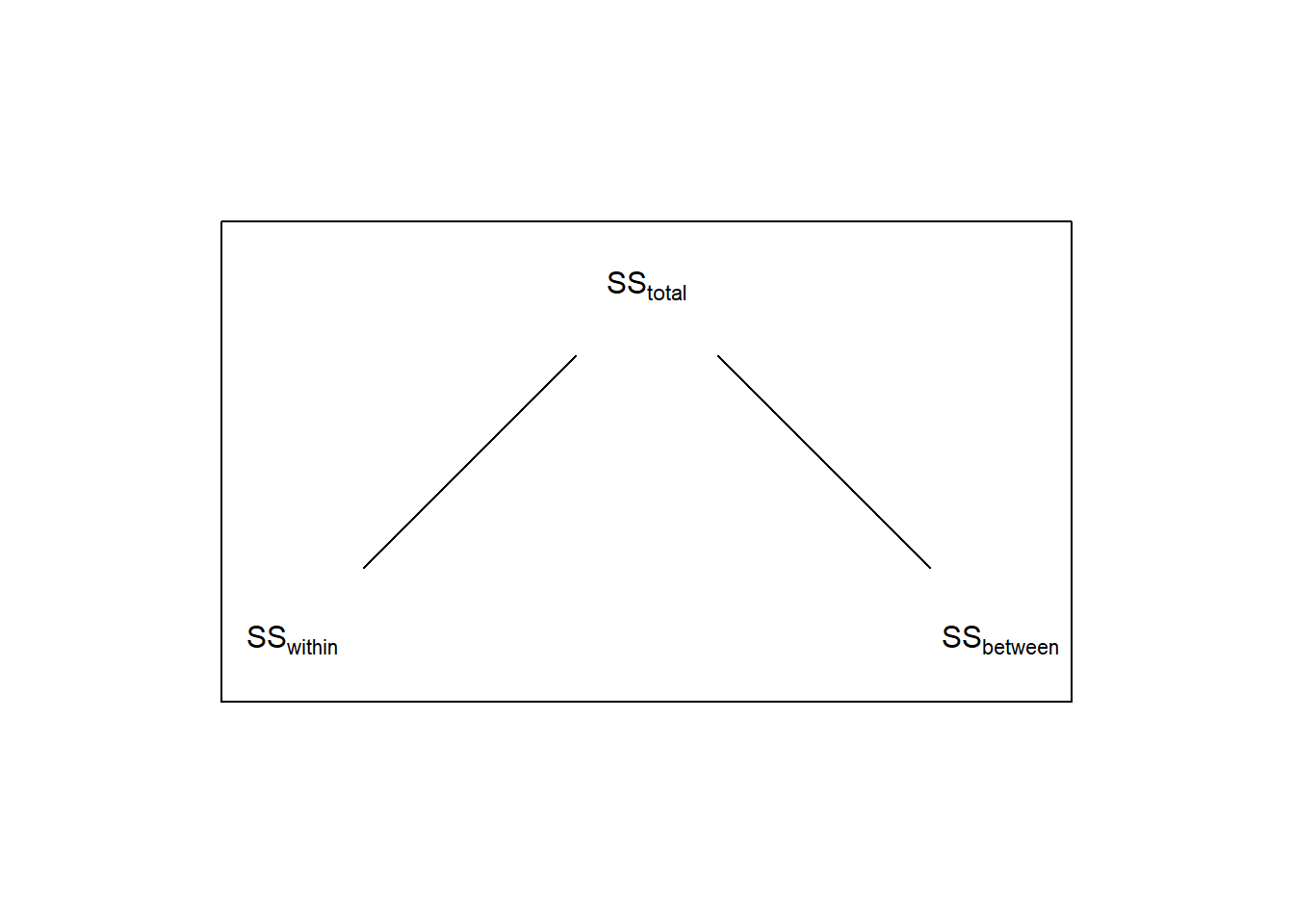
Here, \(SS_{between}\) = 143.4444 reflects the variability across the ‘time’ factor, and \(SS_{within}\) = 715.5 is the variability within each level of time.
You wouldn’t want to analyze a repeated measures design this way because you wouldn’t be taking into account the variability in weights across the subjects. Treated as an independent measures ANOVA, this variability between subjects is part of \(SS_{within}\) (or ‘Residuals’ in R’s output).
Thus, for the denominator of the ANOVA for a repeated measures design we only want the component of \(SS_{within}\) that’s not associated with the variability across subjects. This is done by breaking down \(SS_{within}\) into two components: one component associated with within-subject variability, called \(SS_{subject}\) and the remaining variability called \(SS_{error}\):
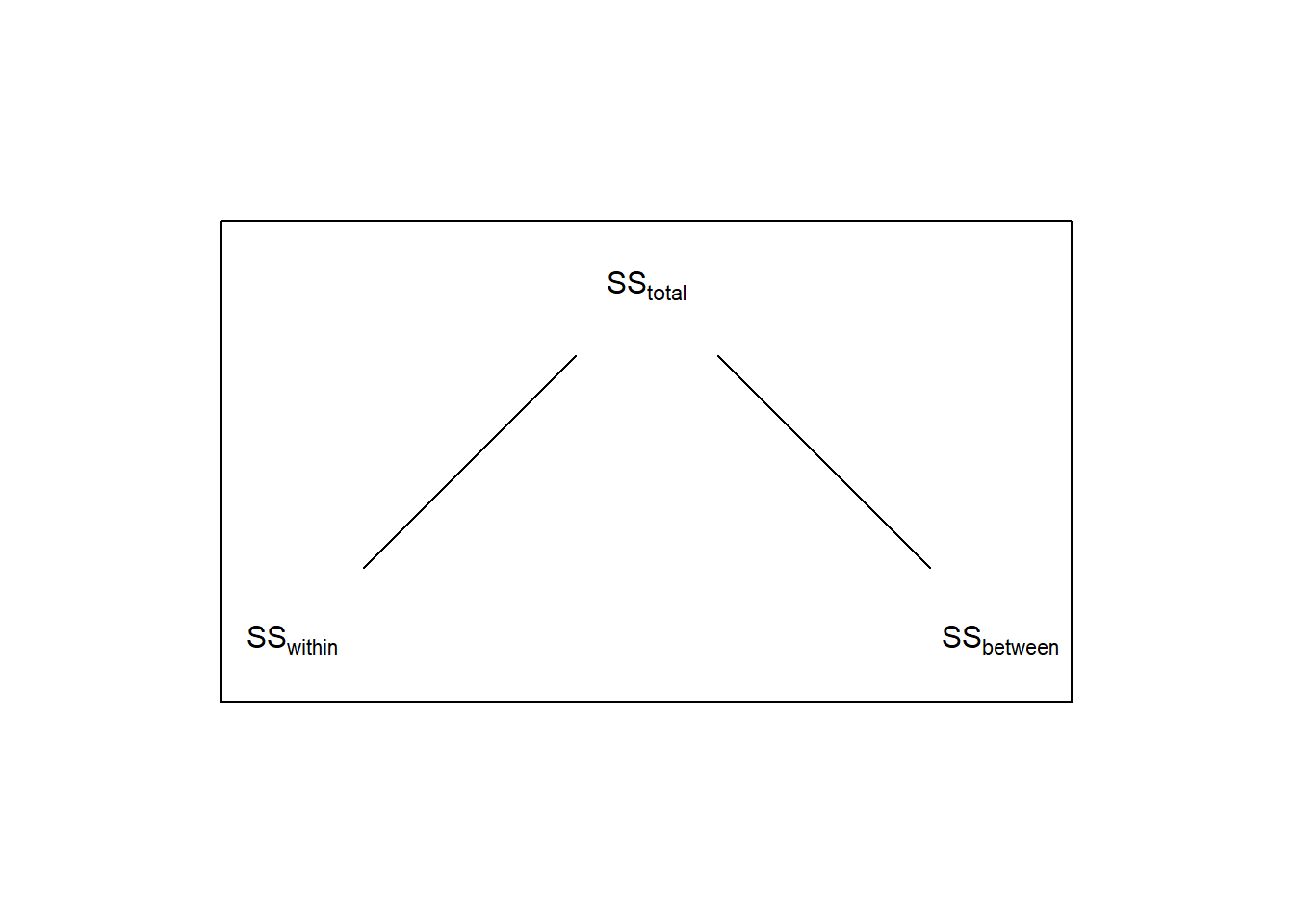
For ANOVA, the way of accounting for this source of variability is to subtract it out of the \(SS_{within}\), which will make the denominator of the F-test smaller, and therefore the F-statistic larger.
We can calculate \(SS_{subject}\) in R by doing something a little weird - we’ll run another one-factor ANOVA, but this time with ‘subject’ as our factor. We’ll pull out the SS and Df from this analysis and call them \(SS_{subject}\) and \(df_{subject}\):
## Analysis of Variance Table
##
## Response: weight
## Df Sum Sq Mean Sq F value Pr(>F)
## subject 5 658.28 131.656 7.8731 0.001706 **
## Residuals 12 200.67 16.722
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The p-value isn’t important here - it’s just telling us the significance of the variability across the the subjects’ weights after averaging across the three time conditions.
20.2.3 The denominator for the repeated measures ANOVA: \(SS_{error}\)
\(SS_{subject}\) is the sums of squared deviation of each subject from the grand mean, and is exactly the source of variability that we want to remove from our analysis.
For repeated measures ANOVA we do this by literally subtracting \(SS_{subject}\) from \(SS_{within}\) in the original independent measures ANOVA. We call this new sums of squared \(SS_{error}\)
\[SS_{error} = SS_{within} - SS_{subject}\]
which, for our example is:
## [1] 57.22222\(SS_{error}\) will serve as the sums-of-squares for the denominator for the repeated-measures ANOVA. To calculate \(MS_{error}\) we need to divide by the degrees of freedom for \(SS_{error}\). This is done in the same way as for sums-of-squared error:
\[df_{error} = df_{within} - df_{subject}\]
Which is, for our example:
The new denominator is:
## [1] 5.722222The F-statistic for the repeated measures uses the \(MS_{betweeen}\) from the original independent measures ANOVA for the numerator, but instead uses \(MS_{error}\) for the new denominator:
## [1] 12.53398Finally the p-value is calculated using the appropriate degrees of freedom:
## [1] 0.001885591After subtracting the between-subject variability for the subjects, our F-test has become statistically significant.
20.3 Repeated measures ANOVA with R
The lm function that we used for independent measures ANOVA can’t deal with repeated measures designs. But there are a few packages out there that can. I’m going to use the most general version, called lmer from the lme4 package. For reasons we’ll discuss later, we also have to include the lmerTest package because the creators of lmer are opposed to providing p-values - again more on that later when we get into linear regression.
Once you have the packages installed, the use of lmer is much like it was for lm where we define the ‘model’ as weight ~ time. But now we have to tell the function which factor defines our subject with + (1|subject). It might help to think of (1|subject) as a fraction, where subject is in the denominator - like how we subtracted \(SS_{subject}\) from \(SS_{within}\) to make the new denominator for the repeated measures ANOVA.
## Type III Analysis of Variance Table with Satterthwaite's method
## Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
## time 143.44 71.722 2 10 12.534 0.001886 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1You should recognize the SS, MS, df F and p-value from the analysis that we did by hand.
Don’t worry about the ‘Satterthwaite’s method’ thing for now. It’s a way of dealing with unbalanced designs. We’ll get into this once we’ve learned more about linear regression.
Here’s how to pull out the values in the output to make an APA formatted string:
sprintf('F(%g,%g) = %5.4f, p = %5.4f',
anova.out.3$NumDF,anova.out.3$DenDF,anova.out.3$`F value`,anova.out.3$`Pr(>F)`)## [1] "F(2,10) = 12.5340, p = 0.0019"20.4 Sphericity
Remember, for ANOVA, we assume homogeneity of variance, which is the assumption that the samples of each of our cells are drawn from populations that have equal variance - even if the null hypothesis is false. We’ve discussed earlier that this assumption is fundamenental to the ANOVA hypothesis test.
For repeated measures ANOVA, a related but stronger assumption needs to be met. This is called sphericity. Sphericity is the condition where the variances of the differences between all combinations of related groups (levels) are equal. In our example, the asssumption of sphericity could be violated if perhaps weights stabilize within subjects bewteen three months and six months, so there is more variability in the differences between the first two time-points as the second and third time points in the experiment.
Let’s look at our example.
| Before | After Three Months | After Six Months | 2-1 | 3-1 | 3-2 | |
|---|---|---|---|---|---|---|
| S1 | 45 | 50 | 55 | 5 | 10 | 5 |
| S2 | 42 | 42 | 45 | 0 | 3 | 3 |
| S3 | 36 | 41 | 43 | 5 | 7 | 2 |
| S4 | 39 | 35 | 40 | -4 | 1 | 5 |
| S5 | 51 | 55 | 59 | 4 | 8 | 4 |
| S6 | 44 | 49 | 56 | 5 | 12 | 7 |
Here’s a table of the variances for each column of this table:
| Before | After Three Months | After Six Months | 2-1 | 3-1 | 3-2 | |
|---|---|---|---|---|---|---|
| \(s^{2}\) | 26.97 | 53.07 | 63.07 | 13.9 | 17.37 | 3.07 |
With homogeneity of variance, the first three variance measures should be about the same. They vary by a factor of about two which seems large, but by now you should appreciate that it’s actually not unusual for a sample size this small.
Under sphericity, the next three variances should be about the same. (Technically, sphericity is based on variability in the off-diagonals of the covariance matrix of the data, but the intuition is the same).
Violations of sphericity lead to inflated values of F, and therefore more type I errors than what is expected from the tables.
20.4.1 Mauchly’s test of Sphericity
The standard way to test for a violation of sphericity is ‘Mauchly’s Test of Sphericity’. We won’t go into the details here except to say that it is a \(\chi{2}\) test with k-1 degrees of freedom. If this test turns out statistically significant, it means that there’s a violation of sphericity in your data, which can lead to inflated p-values.
There are at least three modifications of the ANOVA that correct for violations of sphericity: the ‘Greenhouse-Geisser’, the ‘Huyn-Feldt’, and the ‘Lower-bound’ (SPSS provides all three). All three work by decreasing degrees of freedom of both the numerator and the denominator by a multiplicative factor. You still use the F-statistic from the original repeated measures ANOVA. The result is that the F statistic stays the same but the critical values go down and p-values go up. The field seems to be settling on the ‘Greenhouse-Geisser’ correction as the default correction for sphericity.
I’ve been down some rabbit holes to find the most natural way to deal with sphericity (see this useful reference). I’ve settled on the anova_test function in the package ‘rstatix’. You tell it your dependent variable dv = weight, the name for the subject field wid = subject and the within-subject variable within = time:
## ANOVA Table (type III tests)
##
## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 1 time 2 10 12.534 0.002 * 0.167
##
## $`Mauchly's Test for Sphericity`
## Effect W p p<.05
## 1 time 0.434 0.188
##
## $`Sphericity Corrections`
## Effect GGe DF[GG] p[GG] p[GG]<.05 HFe DF[HF] p[HF] p[HF]<.05
## 1 time 0.638 1.28, 6.38 0.009 * 0.76 1.52, 7.6 0.005 *Three separate tables are printed out. The first is the result of the repeated measures ANOVA which (thankfully) matches the results from anova(lmer(..)). The second is the result from Mauchly’s test of sphericity. You can pull out the p-value from the table like this:
## NULLIf this p-value is small, then it is suggested that you use a correction for sphericity, which could be either the Greenhouse-Geisser or the Huynh-Feldt correction. The results from both are in the third table. Both the Greenhouse-Geisser and the Huynh-Feldt corrections recalculate the p-value using the original repeated measures ANOVA F-value, but reducing both \(df_{between}\) and \(df_{error}\) by a multiplicative factor.
20.4.2 Greenhouse-Geisser correction
Here’s how to access the multiplicative factor from the Greenhouse-Geisser correction:
## [1] 0.638You can report the results of the Greenhouse-Geisser correction in APA format using this:
sprintf('F(%s) = %5.4f, p = %5.4f',
anova.out$`Sphericity Corrections`$`DF[GG]`,
anova.out$ANOVA$F,
anova.out$`Sphericity Corrections`$`p[GG]`)## [1] "F(1.28, 6.38) = 12.5340, p = 0.0090"Just for sanity, let’s check that we get our new p-value after adjusting the df’s with the Greenhouse-Geisser factor:
GGe <- anova.out$`Sphericity Corrections`$GGe
# scale the original df's by G
df_between_new <- GGe*df_between
df_error_new <- GGe*df_error
F_orig <- anova.out.3$`F value`
1-pf(F_orig,df_between_new,df_error_new)## [1] 0.009000177It matches the p-value from the Greenhouse-Geisser correction. So although this factor ‘G’ is mysterious, at least we know where the adjusted p-value comes from once we have it.
20.4.3 Huynh-Feldt correction
A similar procedure can be used to access the results of the Huynh-Feldt correction:
sprintf('F(%s) = %5.4f, p = %5.4f',
anova.out$`Sphericity Corrections`$`DF[HF]`,
anova.out$ANOVA$F,
anova.out$`Sphericity Corrections`$`p[HF]`)## [1] "F(1.52, 7.6) = 12.5340, p = 0.0050"Which can be done manually by scaling the degrees of freedom by the ‘HFe’ factor:
Hfe <- anova.out$`Sphericity Corrections`$HFe
# scale the original df's by HFe
df_between_new <- Hfe*df_between
df_error_new <- Hfe*df_error
F_orig <- anova.out.3$`F value`
1-pf(F_orig,df_between_new,df_error_new)## [1] 0.005288238Which matches the p-value from the Huynh-Feldt correction.
For our example, since Mauchly’s test of sphericity was not significant, we can use the usual within-subjects method and reject our null hypothesis with the p-value from the regular repeated measures ANOVA. Otherwise, we’d base our decision on the p-value from one of the two corrections.
Which correction to use? According to Wikipedia: ‘As a general rule of thumb, the Greenhouse–Geisser correction is the preferred correction method when the epsilon estimate is below 0.75. Otherwise, the Huynh–Feldt correction is preferred.’. I have no idea why.
20.5 Apriori contrasts for repeated measures ANOVA
There isn’t a concensus on how Apriori and post hoc comparisons should be made with the repeated measures ANOVA. Since the difference between repeated measures and independent measures ANOVAs is the denominator, or ‘error’ term, you’d think that contrasts for repeated measures ANOVA would be the same as for indepenent, except that you’d use \(MS_{error}\) instead of \(MS_{within}\) in the denominator. However, apparently, this approach is too sensitive to violations of the assumption of sphericity.
Instead, when comparing two means, statisticians (for example Howell) suggest that you simply run independent measures t-tests (or independent measures ANOVAS) on each pair of means. These tests will only use a subset of the data for the denominator which gives you less power (fewer degrees of freedom in the denominator), but will be less biased due to issues with sphericity. Of course, you will also have to correct for familywise error using your favorite method, like Bonferroni.