Chapter 19 Two Factor ANOVA
The Two-factor ANOVA is a hypothesis test on means with a ‘crossed design’ which has two independent variables. Observations are made for all combinations of levels for each of the two variables.
You can find this test in the flow chart here:
We’ll build up to the two-factor ANOVA by starting with what we already know - a 1-factor ANOVA experiment.
19.1 1-factor ANOVA Beer and Caffeine
Suppose you want to study the effects of beer and caffeine on response times for a simple reaction time task. One way to do this is to divide subjects in to four groups: a control group, a group with caffeine (and no beer), a group with beer (and without caffeine), and a lucky group with both beer and caffeine.
We’ll load in this existing data from the course website:
Here are the summary statistics from this data set:
The four conditions, or ‘levels’ are “no beer, no caffeine”, “no beer, caffeine”, “beer, no caffeine”, and “beer, caffeine”
| mean | n | sd | sem | |
|---|---|---|---|---|
| no beer, no caffeine | 1.650833 | 12 | 0.6725455 | 0.1941472 |
| no beer, caffeine | 1.351667 | 12 | 0.4829235 | 0.1394080 |
| beer, no caffeine | 2.210000 | 12 | 0.3476153 | 0.1003479 |
| beer, caffeine | 1.858333 | 12 | 0.4696194 | 0.1355675 |
Here’s a plot of the means with error bars as the standard error of the mean:
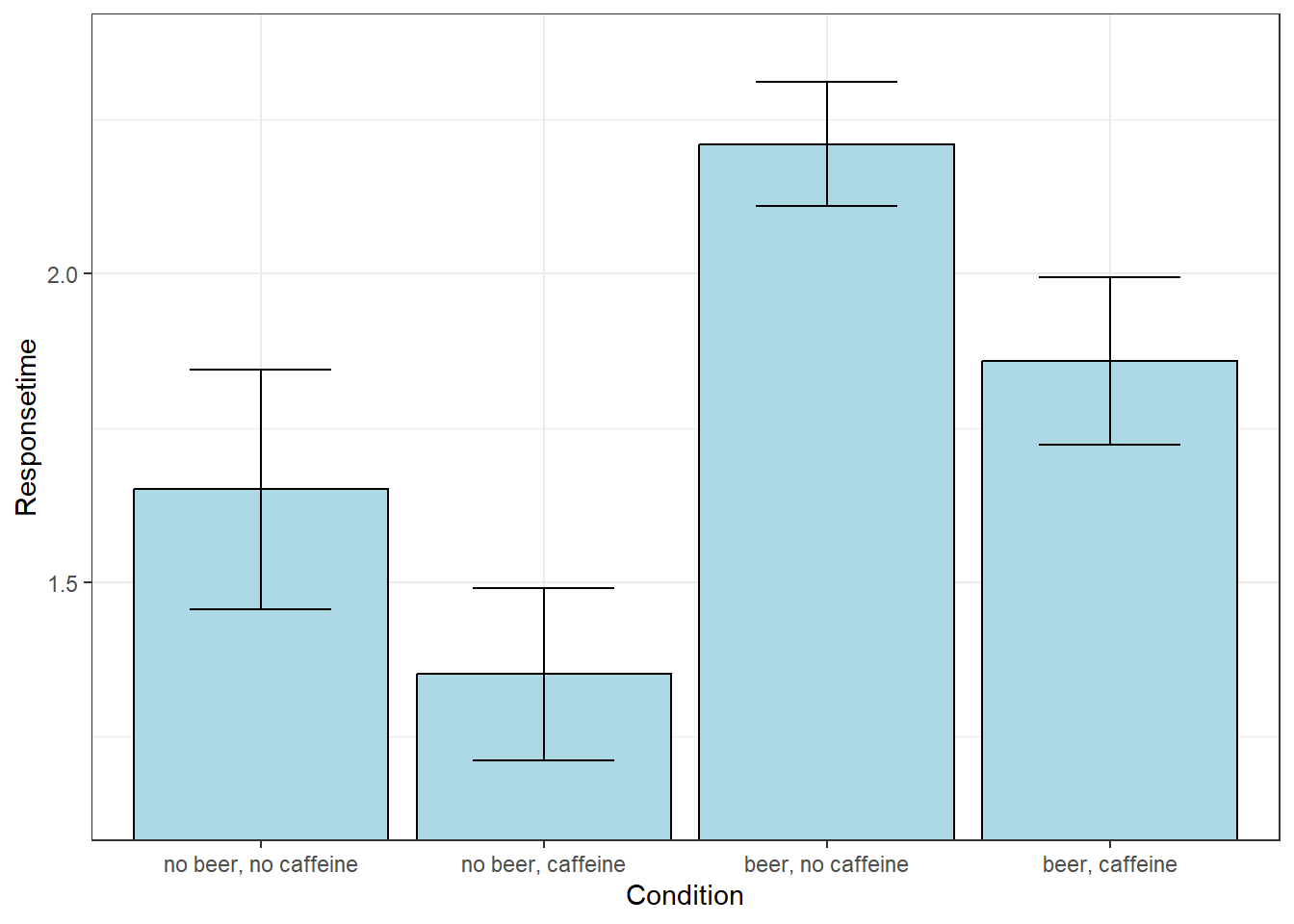
It looks like the means do differ from one another. Here’s the ‘omnibus’ ANOVA result:
| df | SS | MS | F | p | |
|---|---|---|---|---|---|
| Between | 3 | 4.687 | 1.5623 | 6.0856 | p = 0.0015 |
| Within | 44 | 11.296 | 0.2567 | ||
| Total | 47 | 15.983 |
Yup, some combination of beer and caffeine have a significant effect on response times.
In this design we actually manipulated two factors - beer, and caffeine. It’d be nice to be able to look at these two ‘factors’ separately.
19.2 Effect of Beer
Consider the effect of Beer on reaction times. We could just run a t-test on the ‘no beer, no caffeine’ condition vs. the ‘beer, no caffeine’ condition. But we also can compare the ‘no beer, caffeine’ condition to the ‘beer, caffeine’ condition. Or, perhaps even better, we can combine these two comparisons. This combined analysis can be done with a contrast with the following weights:
| no beer, no caffeine | no beer, caffeine | beer, no caffeine | beer, caffeine | |
|---|---|---|---|---|
| Effect of Beer | 1 | 1 | -1 | -1 |
This measures the effect of beer averaging across the two caffeine conditions.
The calculations for this contrast yields:
\[\psi = (1)( 1.65) + (1)( 1.35) + (-1)( 2.21) + (-1)( 1.86) = -1.0658\]
\[MS_{contrast} = \frac{(-1.0658)^{2}}{\frac{(1)^{2}}{12} + \frac{(1)^{2}}{12} + \frac{(-1)^{2}}{12} + \frac{(-1)^{2}}{12}} = 3.4080\]
\[F(1,44) = \frac{3.4080}{0.2567} = 13.2748\]
\[p = 0.0007\]
It looks like there’s a significant effect of beer on response times. Since we’re subtracting the beer from the without beer conditions, our negative value of \(\psi\) indicates that the responses times for beer are greater than for without Beer. Beer increases response times.
19.3 Effect of Caffeine
To study the effect of caffeine, averaging across the two beer conditions, we use this contrast, which is independent of the first one:
| no beer, no caffeine | no beer, caffeine | beer, no caffeine | beer, caffeine | |
|---|---|---|---|---|
| Effect of Caffeine | 1 | -1 | 1 | -1 |
The calculations for this contrast yields:
\[\psi = (1)( 1.65) + (-1)( 1.35) + (1)( 2.21) + (-1)( 1.86) = 0.6508\]
\[MS_{contrast} = \frac{(0.6508)^{2}}{\frac{(1)^{2}}{12} + \frac{(-1)^{2}}{12} + \frac{(1)^{2}}{12} + \frac{(-1)^{2}}{12}} = 1.2708\]
\[F(1,44) = \frac{1.2708}{0.2567} = 4.9498\]
\[p = 0.0313\]
Caffeine has a significant effect on response times - this time \(\psi\) is positive, so response times for without caffeine are greater than for with caffeine. Caffeine reduces response times.
19.4 The Third Contrast: Interaction
For four levels or groups, there should be three independent contrast. Here’s the third contrast:
| no beer, no caffeine | no beer, caffeine | beer, no caffeine | beer, caffeine | |
|---|---|---|---|---|
| Beer X Caffeine | 1 | -1 | -1 | 1 |
What does that third contrast measure? Symbolically, the contrast combines the conditions as:
[without beer without caffeine] - [without beer with caffeine] - [with beer without caffeine] + [with beer with caffeine]
Rearanging the terms as a difference of differences:
([with beer without caffeine] - [without beer without caffeine]) - ([with beer with caffeine]-[without beer with caffeine])
The first difference is the effect of beer without caffeine. The second difference is the effect of beer with caffeine. The difference of the differences is a measure of how the effect of beer changes by adding caffeine. In statistical terms, we call this the interaction between the effects of beer and caffeine on response times. Interactions are labeled with an ‘X’, so this contrast is labeled as ‘Beer X Caffeine’.
You might have noticed the parallel between this and the \(\chi^{2}\) test of independence. This is the same concept, but for means rather than frequencies.
The results of the F-tests for this third contrast is:
\[\psi = (1)( 1.65) + (-1)( 1.35) + (-1)( 2.21) + (1)( 1.86) = -0.0525\]
\[MS_{contrast} = \frac{(-0.0525)^{2}}{\frac{(1)^{2}}{12} + \frac{(-1)^{2}}{12} + \frac{(-1)^{2}}{12} + \frac{(1)^{2}}{12}} = 0.0083\]
\[F(1,44) = \frac{0.0083}{0.2567} = 0.0322\]
\[p = 0.8584\]
We fail to reject \(H_{0}\), so there is no significant interaction between the effects of beer and caffeine on response times. This means that beer effectively increases response times the same amount, regardless of caffeine. Conversely, caffeine reduces response times effectively the same amount with or without beer. Notice the use of the word ‘effectively’ here. We should be careful about saying that ‘beer increases response times the same amount, regardless of caffeine’ because this isn’t true. There is a slight numerical difference, but it is not statistically significant.
19.5 Partitioning \(SS_{between}\)
Recall that for a 1-factor ANOVA, \(SS_{total}\) is broken down in to two parts \(SS_{within}\) and \(SS_{between}\):
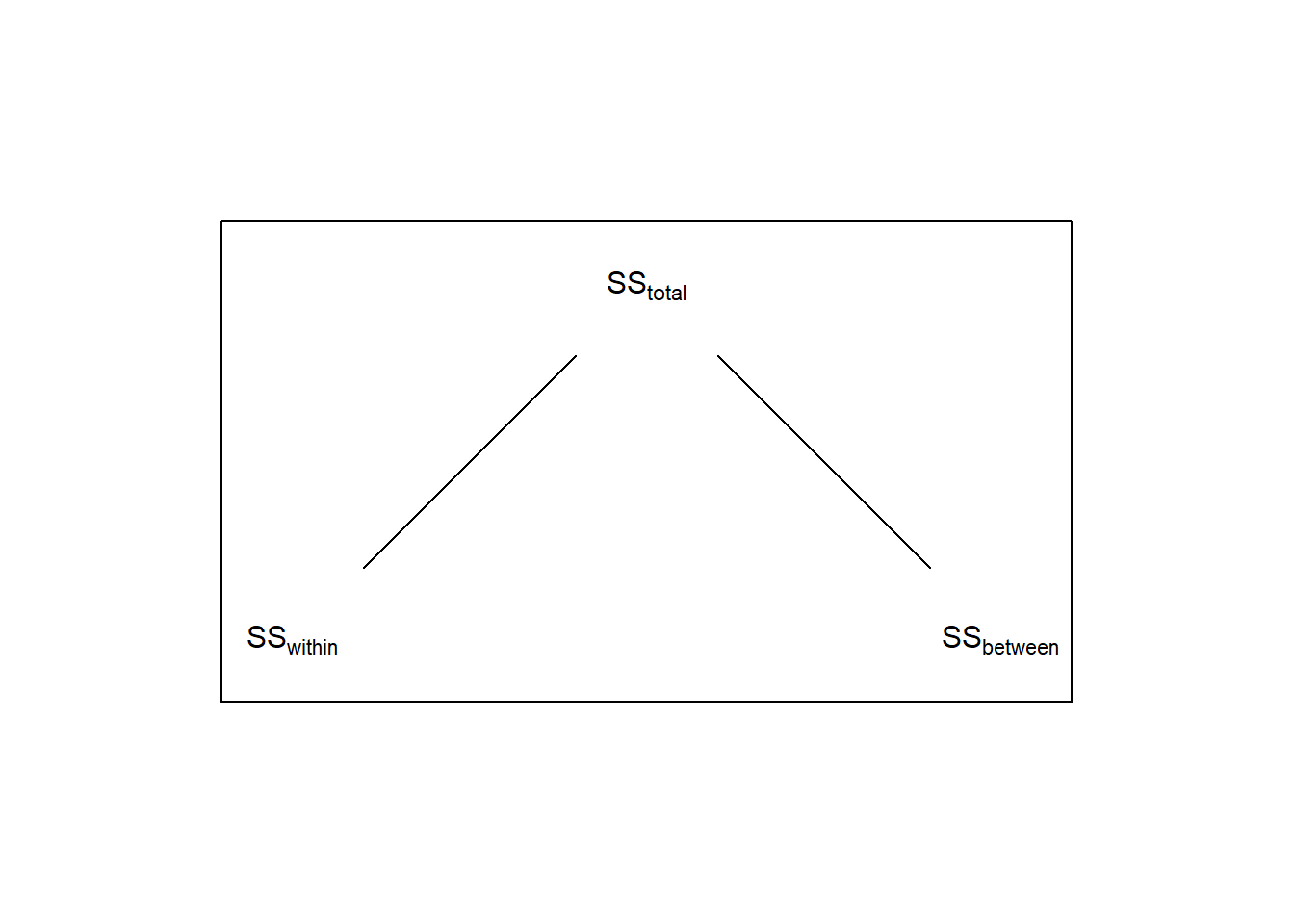
In the chapter section 18.3.1 on APriori and post-hoc tests we discussed how the sums of squared for independent contrasts is a way of breaking down the total variability between the means, \(SS_{between}\). The same is true here for our three orthogonal contrasts. Summing up the three \(SS_{contrast}\) values gives us:
\[3.408+1.2708+0.0083 = 4.6871 = SS_{between}\]
So the three contrasts have partitioned the total variability between the means into three separate tests - each telling us something different about what is driving the significance of the ‘omnibus’ F-test. If we call the sums-of-squares for each of the three contrasts \(SS_{beer}\), \(SS_{caffeine}\), and \(SS_{beerXcaffeine}\) (where the ‘\(X\)’ means ’interaction), we can expand the above diagram to this:

This experiment has what is called a ‘factorial design’, where there are conditions for each combination of levels for the two factors of beer and caffeine. This example is a ‘balanced design’, which means that the sample sizes are the same for all conditions.
A standard way to analyze a factorial design is to break the overall variability between the means into separate hypothesis tests - a main effect for each factor, and their interactions. In this section we’ll show how treating the same data that we just discussed as a 2-factor ANOVA gives us the exact same result as treating the same results as a 1-factor ANOVA with three contrasts.
19.6 2-Factor ANOVA
I’ve saved the same data set but in a way that’s ready to be analyzed as a factorial design experiment. We’ll load it in here:
data.2 <- read.csv('http://courses.washington.edu/psy524a/datasets/BeerCaffeineANOVA2.csv')
head(data.2)## Responsetime caffeine beer
## 1 2.24 no caffeine no beer
## 2 1.62 no caffeine no beer
## 3 1.48 no caffeine no beer
## 4 1.70 no caffeine no beer
## 5 1.06 no caffeine no beer
## 6 1.39 no caffeine no beerThe data format has the same ‘ResponseTime’ column, but now it has two columns instead of one that define which condition for each measurement. The ‘caffeine’ column has two levels: ‘caffeine’ and ‘no caffeine’. Similarly the ‘beer’ column has two levels ‘beer’ and ‘no beer’. This way of storing the data is called ‘long format’, where which each row corresponds to a single observation.
This experiment is called a 2x2 factorial design because each of the two factors has two levels. We can summarize the results in the form of matrices with rows and columns corresponding to the two factors. We’ll set the ‘row factor’ as ‘caffeine’ and the ‘column factor’ as ‘beer’. That is, ‘beer’ varies across the rows and ‘caffeine’ varies across the column. Here’s the 2x2 table for the means:
| no beer | beer | |
|---|---|---|
| no caffeine | 1.6508 | 2.2100 |
| caffeine | 1.3517 | 1.8583 |
Instead of bar graphs, it’s common to plot results of factorial designs as data points with lines connecting them. By default, I plot the column factor along the x-axis and define the row factor in the legend. There are various ways of doing this in R. Here’s an example for our data. It requires both ‘ggplot2’ and the ‘dplyr’ libraries. Both are part of the ‘tidyverse’ package.
# Do this to avoid a stupid useless error message
options(dplyr.summarise.inform = FALSE)
# order the levels for the two factors (alphabetical by default)
data.2$caffeine <- factor(data.2$caffeine,levels = c('no caffeine','caffeine'))
data.2$beer <- factor(data.2$beer,levels = c('no beer','beer'))
# Make a table (tibble) with generic names
summary.table <- data.2 %>%
dplyr::group_by(caffeine,beer) %>%
dplyr::summarise(
m = mean(Responsetime),
sem = sd(Responsetime)/sqrt(length(Responsetime))
)
# plot with error bars, replacing generic names with specific names
ggplot(summary.table, aes(beer, m)) +
geom_errorbar(
aes(ymin = m-sem, ymax = m+sem, color = caffeine),
position = position_dodge(0), width = 0.5)+
geom_line(aes(group = caffeine,color = caffeine)) +
geom_point(aes(group = caffeine,color = caffeine),size = 5) +
scale_color_manual(values = rainbow(2)) +
xlab('beer') +
ylab('Response Time (s)') +
theme_bw()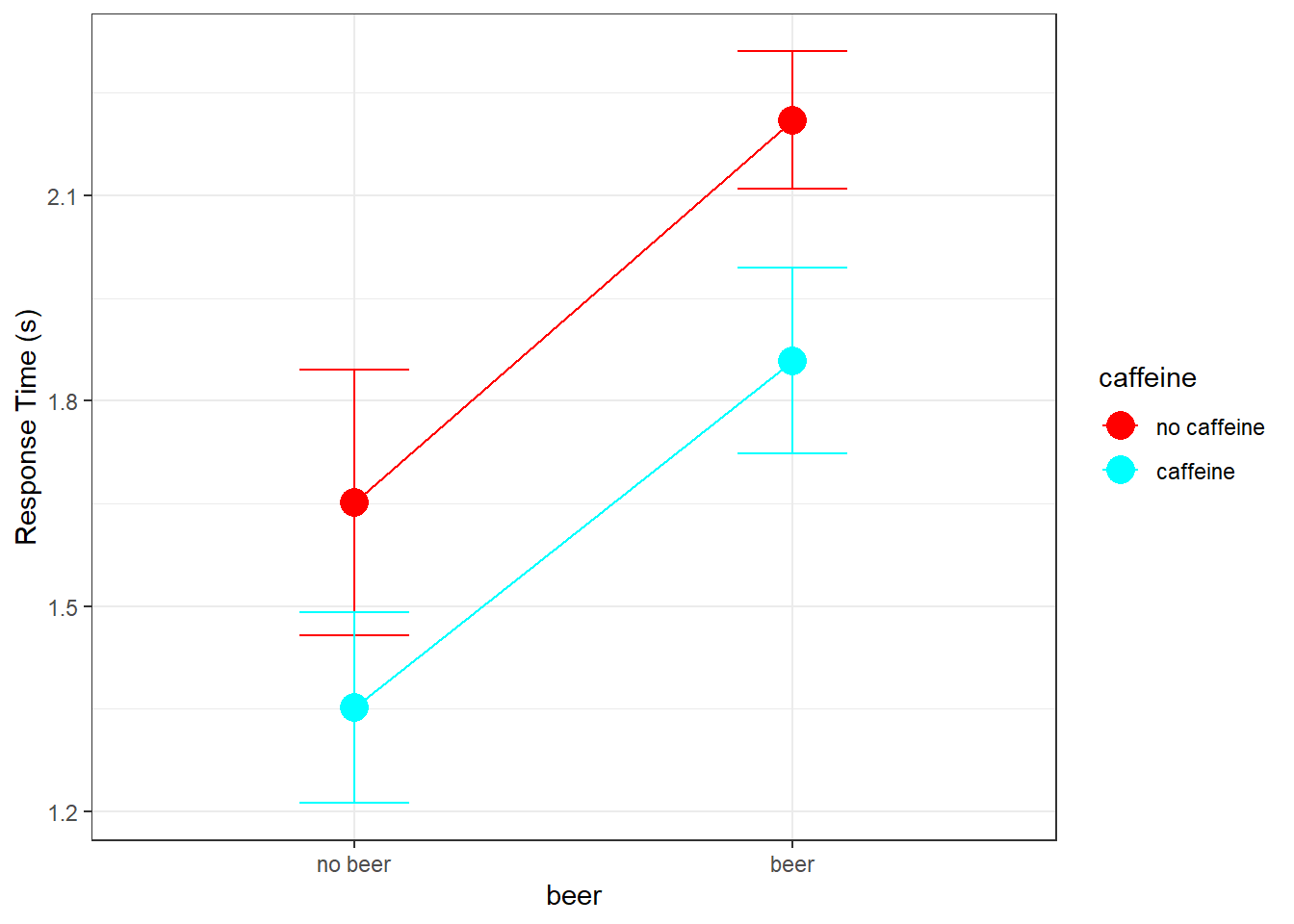
19.7 Within-Cell Variance (\(MS_{wc}\))
The three F-tests for a 2-factor ANOVA will use the same within-cell mean-squared error as the denominator. This is calculated the same way as for the 1-way ANOVA. We first add up the sums of squares for each condition.
The sums of squares within each group is called ‘\(SS_{wc}\)’ where ‘wc’ means ‘within cell’ since we’re now talking about cells in a matrix. Here’s the table for \(SS_{wc}\):
| no beer | beer | |
|---|---|---|
| no caffeine | 4.9755 | 1.3292 |
| caffeine | 2.5654 | 2.4260 |
\(SS_{wc}\) is the sum of these individual within-cell sums of squares:
\[SS_{wc} = 4.9755+2.5654+1.3292+2.426 = 11.2961\]
Each cell contributes n-1 degrees of freedom to \(SS_{wc}\), so the degrees of freedom for all cells is N-k, where k is the total number of cells and N is the total sample size (n \(\times\) k):
\[df_{wc} = 48 - 4 = 44\]
Mean-squared error is, as always, \(\frac{SS}{df}\):
\[MS_{wc} = \frac{SS_{wc}}{df_{wc}} = \frac{11.296}{44} = 0.2567\]
This is the same value and df as \(MS_{w}\) from above when we treated the same data as a 1-factor ANOVA design.
The three contrasts that we used for the 1-factor ANOVA example correspond to what we call ‘main effects’ for the factors and the ‘interaction’ between the factors. To calculate the main effects by hand we need to calculate the means across the rows and columns of our factors. Here’s a table with the row and sum means in the ‘margins’:
| no beer | beer | means | |
|---|---|---|---|
| no caffeine | 1.6508 | 2.2100 | 1.9304 |
| caffeine | 1.3517 | 1.8583 | 1.6050 |
| means | 1.5012 | 2.0342 | 1.7677 |
The bottom-right number is the mean of the means, which is the grand mean (\(\overline{\overline{X}}\) = 1.7677)
19.7.1 Main Effect for Columns (Beer)
Calculating main effects is lot like calculating \(SS_{between}\) for the 1-factor ANOVA. For the main effect for columns, we calculate the sums of squared deviations of the column means from the grand mean, and scale it by the number of samples that contributed to each column mean. For our example, the sums of square deviations is:
\[(1.5012-1.7677)^2+(2.0342-1.7677)^2=0.071+0.071 = 0.142\]
There are \(2 \times 12 = 24\) samples for each column mean, so the sums of squared for the columns, called \(SS_{C}\) is
\[SS_{C} = (24)(0.142) = 3.408\]
Since 2 means contributing to \(SS_{R}\), so the degrees of freedom is \(df_{R}\) = 2 -1 = 1
\(MS_{C}\) is therefore
\[\frac{SS_{C}}{df_{C}} = \frac{3.4080}{1} = 3.4080\]
The F-statistic for this main effect is \(MS_{C}\) divided by our common denominator, \(MS_{wc}\)
\[F = \frac{MS_{C}}{MS_{wc}} = \frac{3.4080}{0.2567} = 13.2748\]
We can calculate the p-value for this main effect using pf:
## [1] 0.0007060154Notice that the F and p-values are the same as for the first contrast in the 1-way ANOVA above. If you work out the algebra you’ll find that the math is the same. The main effect in a multi-factorial ANOVA is exactly the same as the appropriate contrast in a 1-factor ANOVA.
19.7.2 Main Effect for Rows (Caffeine)
The calculations for finding the main effect of rows (Caffeine) on response times is completely analogous to finding the main effect for columns. We use our row means in the table above, which are the averages across the two beer conditions.
The sums of squared deviations for the means for rows is:
\[(1.9304-1.7677)^2+(1.605-1.7677)^2=0.0265+0.0265 = 0.053\]
There are \(2 \times 12 = 24\) samples for each row mean, so the sums of squared for the row, called \(SS_{R}\) is
\[SS_{R} = (24)(0.0529) = 1.2708\]
There are 2 means contributing to \(SS_{R}\), so the degrees of freedom is \(df_{R}\) = 2 -1 = 1
\(MS_{R}\) is therefore
\[\frac{SS_{R}}{df_{R}} = \frac{1.2708}{1} = 1.2708\]
The F-statistic for this main effect is \(MS_{R}\) divided by our common denominator, \(MS_{wc}\)
\[F = \frac{MS_{R}}{MS_{wc}} = \frac{1.2708}{0.2567} = 4.9498\]
The p-value for the main effect of Beer is:
## [1] 0.0312691419.7.3 Interaction Between Beer and Caffeine
The third contrast in the 1-factor ANOVA measured the differential effect of caffeine on response times across the two beer conditions (or vice versa). Recall that for a 1-factor ANOVA the sums of squares associated with three orthogonal conditions adds up to \(SS_{between}\) for four groups. Also, recall that \(SS_{between} + SS_{within} = SS_{total}\).
The easiest way to calculate the sums of square value for interaction is to appreciate that
\[SS_{total} = SS_{caffeine} + SS_{beer} + SS_{caffeineXbeer} + SS_{wc}\]
The total sums of squares is \(SS_{total}\) = 15.983.
Therefore,
\[SS_{caffeineXbeer} = SS_{total} - (SS_{wc} + SS_{caffeine} + SS_{beer})\]
so
\[SS_{RXC} = SS_{total}-SS_{R}-SS_{C}-SS_{wc} = 15.9830 - 1.2708 - 3.4080 - 11.2960 = 0.0083\]
The degrees of freedom for this interaction term is (\(n_{rows}\)-1)*(\(n_{cols}\)-1):
\[df_{RXC} = (n_{rows}-1)(n_{cols}-1) = (2-1)(2-1) = 1\]
So the mean-squared error for the interaction is
\[\frac{SS_{RXC}}{df_{RXC}} = \frac{0.0083}{1} = 0.0083\]
Using \(SS_{wc}\) for the denominator again, the F-statistic is:
$$
The p-value for the interaction is:
## [1] 0.8584132There is not a significant interaction between caffeine and beer on response times. Compare these numbers to the results of the third contrast in the 1-factor ANOVA above.
We typically summarize our calculations and results in a table like this:
| df | SS | MS | F | p | |
|---|---|---|---|---|---|
| caffeine | 1 | 1.2708 | 1.2708 | 4.9498 | p = 0.0313 |
| beer | 1 | 3.4080 | 3.408 | 13.2748 | p = 0.0007 |
| interaction | 1 | 0.0083 | 0.0083 | 0.0322 | p = 0.8584 |
| wc | 44 | 11.2960 | 0.2567 | ||
| Total | 47 | 15.9830 |
Using APA format we state, for our three tests:
There is a main effect of caffeine. F(1,44) = 4.9498, p = 0.0313.
There is a main effect of beer. F(1,44) = 13.2748, p = 0.0007.
There is not a significant interaction between caffeine and beer. F(1,44) = 0.0322, p = 0.8584.
You might have noticed that didn’t use any correction for familywise error for these three tests. There is a general consensus that the main effects and the interaction do not require familywise error correction. But if we treat the same data as a 1-factor design with three planned contrasts, we should apply error correction (like Bonferroni) even though the math and p-values are the same. If you find discrepancies like this baffling you are not alone.
19.8 The two-factor ANOVA in R
Conducting a two-factor ANOVA in R is a lot like for 1-factor ANOVA. We’ll use the lm function and pass it through the anova function to get our table and statistics. The difference is the definition of the formula. Here we’ll use: Responsetime ~ caffieene*beer. The use of ’*’ is the way to ask R to conduct not only the main effect of caffeine and beer but also their interaction:
## Analysis of Variance Table
##
## Response: Responsetime
## Df Sum Sq Mean Sq F value Pr(>F)
## caffeine 1 1.2708 1.2708 4.9498 0.031269 *
## beer 1 3.4080 3.4080 13.2748 0.000706 ***
## caffeine:beer 1 0.0083 0.0083 0.0322 0.858395
## Residuals 44 11.2960 0.2567
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1All of these numbers should look familiar.
19.9 A 2x3 Factorial Example
Factorial designs let you study the effects of one factor across multiple levels of another factor (or factors). In this made-up example, we’ll study the effect of two kinds of diets: “Atkins” and “pea soup” on the systolic blood pressure (BP, in mm Hg) for three exercise levels: “none”, “a little”, and “a lot”. A systolic blood pressure less than 120 mm Hg is considered normal. 20 subjects participated in each of the 2x3 = 6 groups for a total of 120 subjects. Here’s how to load in the data from the course website and order the levels:
# data.3 <- read.csv('http://courses.washington.edu/psy524a/datasets/DietExercise.csv')
# data.3$Diet <- factor(data.3$Diet,levels = c('Atkins','pea soup'))
# data.3$Exercise <- factor(data.3$Exercise,levels = c('none','a little','a lot'))The data is stored in ‘long format’ like this:
| BP | Diet | Exercise |
|---|---|---|
| 125.6032 | Atkins | none |
| 137.7546 | Atkins | none |
| 122.4656 | Atkins | none |
| 158.9292 | Atkins | none |
| 139.9426 | Atkins | none |
| 122.6930 | Atkins | none |
| 142.3114 | Atkins | none |
| 146.0749 | Atkins | none |
| 143.6367 | Atkins | none |
| 130.4192 | Atkins | none |
| 157.6767 | Atkins | none |
| 140.8476 | Atkins | none |
| 125.6814 | Atkins | none |
| 101.7795 | Atkins | none |
| 151.8740 | Atkins | none |
| 134.3260 | Atkins | none |
| 134.7571 | Atkins | none |
| 149.1575 | Atkins | none |
| 147.3183 | Atkins | none |
| 143.9085 | Atkins | none |
| 148.7847 | Atkins | a little |
| 146.7320 | Atkins | a little |
| 136.1185 | Atkins | a little |
| 105.1597 | Atkins | a little |
| 144.2974 | Atkins | a little |
| 134.1581 | Atkins | a little |
| 132.6631 | Atkins | a little |
| 112.9387 | Atkins | a little |
| 127.8277 | Atkins | a little |
| 141.2691 | Atkins | a little |
| 155.3802 | Atkins | a little |
| 133.4582 | Atkins | a little |
| 140.8151 | Atkins | a little |
| 134.1929 | Atkins | a little |
| 114.3441 | Atkins | a little |
| 128.7751 | Atkins | a little |
| 129.0857 | Atkins | a little |
| 134.1103 | Atkins | a little |
| 151.5004 | Atkins | a little |
| 146.4476 | Atkins | a little |
| 132.5321 | Atkins | a lot |
| 131.1996 | Atkins | a lot |
| 145.4545 | Atkins | a lot |
| 143.3499 | Atkins | a lot |
| 124.6687 | Atkins | a lot |
| 124.3876 | Atkins | a lot |
| 140.4687 | Atkins | a lot |
| 146.5280 | Atkins | a lot |
| 133.3148 | Atkins | a lot |
| 148.2166 | Atkins | a lot |
| 140.9716 | Atkins | a lot |
| 125.8196 | Atkins | a lot |
| 140.1168 | Atkins | a lot |
| 118.0596 | Atkins | a lot |
| 156.4954 | Atkins | a lot |
| 164.7060 | Atkins | a lot |
| 129.4917 | Atkins | a lot |
| 119.3380 | Atkins | a lot |
| 143.5458 | Atkins | a lot |
| 132.9742 | Atkins | a lot |
| 171.0243 | pea soup | none |
| 134.4114 | pea soup | none |
| 145.3461 | pea soup | none |
| 135.4200 | pea soup | none |
| 123.8509 | pea soup | none |
| 137.8319 | pea soup | none |
| 107.9256 | pea soup | none |
| 156.9833 | pea soup | none |
| 137.2988 | pea soup | none |
| 167.5892 | pea soup | none |
| 142.1326 | pea soup | none |
| 124.3508 | pea soup | none |
| 144.1609 | pea soup | none |
| 120.9885 | pea soup | none |
| 116.1955 | pea soup | none |
| 139.3717 | pea soup | none |
| 128.3506 | pea soup | none |
| 135.0166 | pea soup | none |
| 136.1151 | pea soup | none |
| 126.1572 | pea soup | none |
| 121.4700 | pea soup | a little |
| 127.9723 | pea soup | a little |
| 147.6713 | pea soup | a little |
| 107.1465 | pea soup | a little |
| 138.9092 | pea soup | a little |
| 134.9943 | pea soup | a little |
| 145.9465 | pea soup | a little |
| 125.4372 | pea soup | a little |
| 135.5503 | pea soup | a little |
| 134.0065 | pea soup | a little |
| 121.8622 | pea soup | a little |
| 148.1180 | pea soup | a little |
| 147.4060 | pea soup | a little |
| 140.5032 | pea soup | a little |
| 153.8025 | pea soup | a little |
| 138.3773 | pea soup | a little |
| 110.8511 | pea soup | a little |
| 121.4010 | pea soup | a little |
| 111.6308 | pea soup | a little |
| 122.8990 | pea soup | a little |
| 110.6945 | pea soup | a lot |
| 120.6317 | pea soup | a lot |
| 106.3362 | pea soup | a lot |
| 122.3704 | pea soup | a lot |
| 110.1812 | pea soup | a lot |
| 146.5093 | pea soup | a lot |
| 130.7506 | pea soup | a lot |
| 133.6526 | pea soup | a lot |
| 125.7628 | pea soup | a lot |
| 145.2326 | pea soup | a lot |
| 110.4640 | pea soup | a lot |
| 113.0753 | pea soup | a lot |
| 141.4842 | pea soup | a lot |
| 110.2396 | pea soup | a lot |
| 116.8893 | pea soup | a lot |
| 114.1079 | pea soup | a lot |
| 115.2001 | pea soup | a lot |
| 115.8133 | pea soup | a lot |
| 127.4128 | pea soup | a lot |
| 117.3400 | pea soup | a lot |
Here’s a plot of the means with error bars:
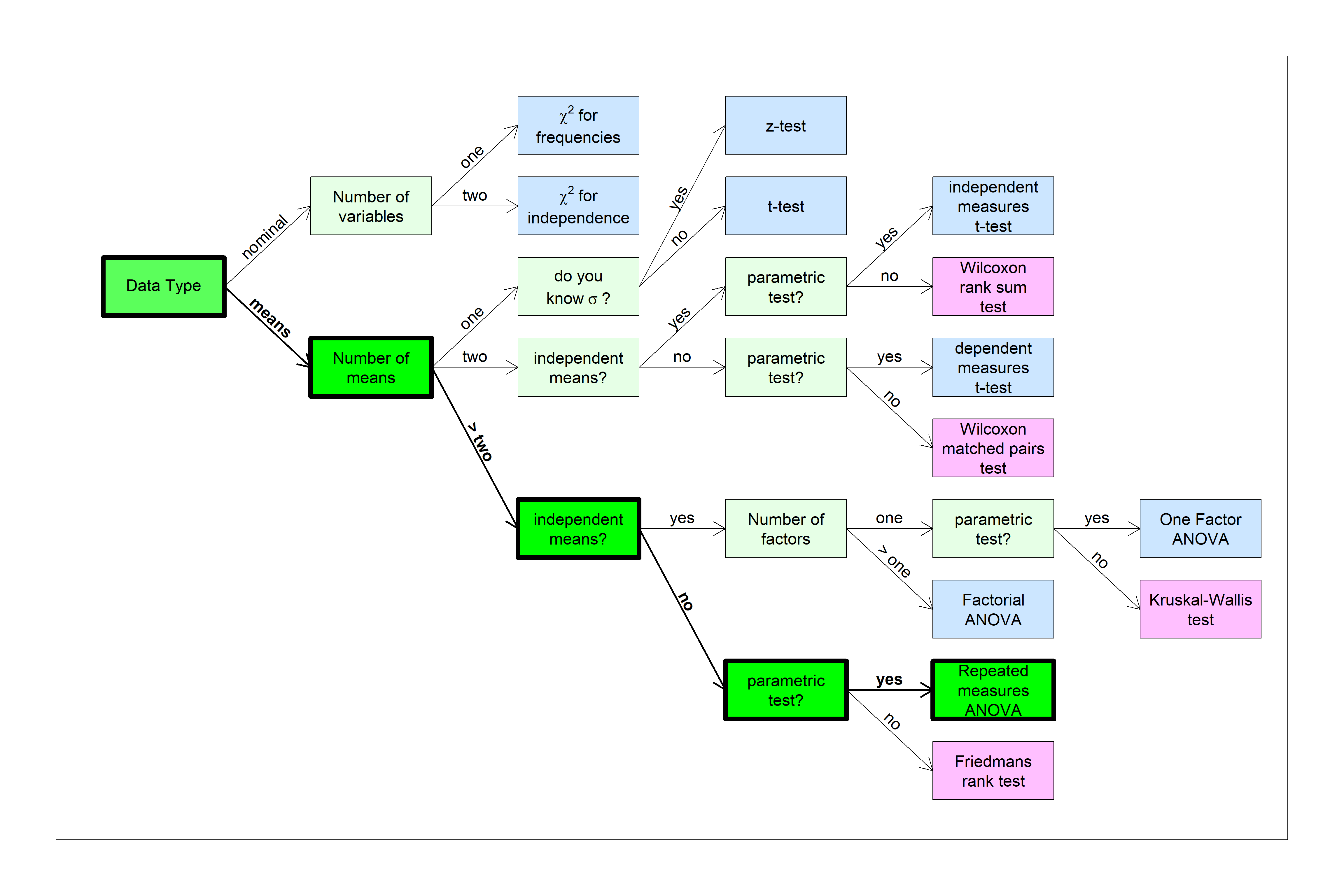
Here we’ve defined the row factor to be Diet and the column factor to be Exercise.
From the graph it looks like the Atkins diet has little effect on systolic blood pressure across exercise levels, but the pea soup diet does seem to lead to lower BP for higher levels of exercise.
The math behind running a 2-factor ANOVA on this design is the same as for the 2x2 example above.
19.9.1 Calculating \(MS_{wc}\) for the 2x3 example
\(SS_{wc}\) and \(MS_{wc}\) are calculated the same way as for the 2x2 example. We sum up the sums of squared deviation of each score from the mean of the cell that each score came from. Here’s the table of the SS for each of the cells:
| none | a little | a lot | |
|---|---|---|---|
| Atkins | 3565.484 | 3245.913 | 2802.910 |
| pea soup | 4715.587 | 3546.061 | 2834.728 |
\(SS_{wc}\) is therefore
\[3565.48+4715.59+3245.91+3546.06+2802.91+2834.73 = 20710.7\]
Again, each cell contributes n- 1 degrees of freedom to \(SS_{wc}\), so the degrees of freedom for all cells is N-k, where k is the total number of cells and N is the total sample size (n \(\times\) k):
\[df_{wc} = 120 - 6 = 114\]
Mean-squared within-cell is:
\[MS_{wc} = \frac{SS_{wc}}{df_{wc}} = \frac{2.0710683\times 10^{4}}{114} = 181.6727\]
Remember this number: \(MS_{wc}\) = 181.6727. It will be the common denominator for all of the F-tests for this data set.
Like for the 2x2 example, the main effects are done by computing the sums of squared deviation from the rows and column means from the grand mean, weighted by the total number of subjects contributing to each row or column mean.
Here’s a table of the means, along with the row and column means:
| none | a little | a lot | means | |
|---|---|---|---|---|
| Atkins | 137.8579 | 134.9029 | 137.0820 | 136.6142 |
| pea soup | 136.5260 | 131.7978 | 121.7074 | 130.0104 |
| means | 137.1920 | 133.3503 | 129.3947 | 133.3123 |
19.9.2 Main effect for columns (Exercise)
The main effect of columns (Exercise), the sums of squared deviation from the grand mean is:
\[\small (137.192-133.312)^2+(133.35-133.312)^2+(129.395-133.312)^2=15.0521+0.0014+15.3476 = 30.4011\]
Since there are 2 levels for the row factor, there are 20 \(\times\) 2 = 40 subjects for each column mean. So \(SS_{col}\) is:
\[SS_{C} = (40)(30.4011) = 1216.032\]
There are 3 means contributing to \(SS_{C}\), so the degrees of freedom is \(df_{C}\) = 2 -1 = 1
\(MS_{C}\) is therefore
\[\frac{SS_{C}}{df_{C}} = \frac{1216.0320}{2} = 608.0160\]
The F-statistic for this main effect is \(MS_{C}\) divided by our common denominator, \(MS_{wc}\)
\[F = \frac{MS_{C}}{MS_{wc}} = \frac{608.0160}{181.6727} = 3.3468\]
The p-value for the main effect of Exercise is:
## [1] 0.0386878719.9.3 Main effect for rows (Diet)
The main effect of rows (Diet), the sums of squared deviation from the grand mean is:
\[(136.614-133.312)^2+(130.01-133.312)^2=10.9025+10.9025 = 21.805\]
This time, since there are 3 levels for the column factor, there are 20 \(\times\) 3 = 60 subjects for each row mean. So \(SS_{row}\) is:
\[SS_{R} = (60)(21.8051) = 1308.3198\]
There are 2 means contributing to \(SS_{R}\), so the degrees of freedom is \(df_{R}\) = 3 -1 = 2
\(MS_{R}\) is therefore
\[\frac{SS_{R}}{df_{R}} = \frac{1308.3198}{1} = 1308.3198\]
The F-statistic for this main effect is \(MS_{R}\) divided by our common denominator, \(MS_{wc}\)
\[F = \frac{MS_{R}}{MS_{wc}} = \frac{1308.3198}{181.6727} = 7.2015\]
The p-value for the main effect of Diet is:
## [1] 0.00836890919.9.4 Interaction Between Diet and Exercise
The total sums of squares is 2.4404637^{4}, so we can calculate \(SS_{RXC}\) by;
\[SS_{RXC} = SS_{total}-SS_{R}-SS_{C}-SS_{wc} = 24404.6372 - 1308.3198 - 1216.0320 - 20710.6827 = 1169.6028\]
The degrees of freedom for this interaction term is:
\[df_{RXC} = (n_{rows}-1)(n_{cols}-1) = (2-1)(3-1) = 2\]
The mean-squared error for the interaction is
\[\frac{SS_{RXC}}{df_{RXC}} = \frac{1169.6028}{2} = 584.8014\]
Using \(SS_{wc}\) for the denominator again, the F-statistic is:
\[F = \frac{MS_{RXC}}{MS_{wc}} = \frac{584.8014}{181.6727} = 3.2190\]
The p-value for the interaction is:
## [1] 0.04365711Here’s how to run the 2-factor ANOVA in R:
## Analysis of Variance Table
##
## Response: BP
## Df Sum Sq Mean Sq F value Pr(>F)
## Diet 1 1308.3 1308.32 7.2015 0.008369 **
## Exercise 2 1216.0 608.02 3.3468 0.038689 *
## Diet:Exercise 2 1169.6 584.80 3.2190 0.043658 *
## Residuals 114 20710.7 181.67
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Using APA format we’d say:
There is a main effect of Diet. F(1,114) = 7.2015, p = 0.0084.
There is a main effect of Exercise. F(2,114) = 3.3468, p = 0.0387.
There is a significant interaction between Diet and Exercise. F(2,114) = 3.2190, p = 0.0437.
All three hypothesis tests are statistically significant, but this doesn’t really tell us much about what’s driving the effects of Diet and Exercise on BP. As discussed above when we plotted the results, what seems to be happening is that only the subjects on the pea soup diet are influenced by Exercise.
It might make sense, instead, to run two ANOVAs on the data, one for the Atkins diet and one for the pea soup diet. We expect to find that most of variability across the means is driven by the effect of Exercise for the pea soup dieters.
19.10 Simple Effects
Running ANOVAs on subsets of the data like this is called a simple effects analysis. Running separate ANOVAs on each level of Diet is studying the simple effects of Exercise by Diet. I remember this by replacing the word ‘by’ with ‘for every level of’. That is, this simple effect analysis is studying the effect of Exercise on BP for every level of Diet.
Running simple effects is almost as simple as running separate ANOVA’s for each level of Diet. In fact, let’s start there. We can use the subset function to pull out the data for each of the two diets”:
# Atkins diet:
anova3.out.Atkins <- anova(lm(BP ~ Exercise,data = subset(data.3,Diet == 'Atkins') ))
anova3.out.Atkins## Analysis of Variance Table
##
## Response: BP
## Df Sum Sq Mean Sq F value Pr(>F)
## Exercise 2 93.9 46.939 0.2783 0.7581
## Residuals 57 9614.3 168.672# pea soup diet:
anova3.out.peasoup <- anova(lm(BP ~ Exercise,data = subset(data.3,Diet == 'pea soup') ))
anova3.out.peasoup## Analysis of Variance Table
##
## Response: BP
## Df Sum Sq Mean Sq F value Pr(>F)
## Exercise 2 2291.8 1145.88 5.8862 0.004744 **
## Residuals 57 11096.4 194.67
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1There’s one more think we can do to increase the power of these tests. If we assume homogeneity of variance, then it makes sense to use the denominator of the two-factor ANOVA, \(MS_{wc}\) = 181.6727, for both of these F-tests since this should be a better estimate of the population variance - and it has a larger df which helps with power.
R doesn’t have a function for simple effects, but it’s not hard to do it by hand. All we need to do is pull out \(MS_{wc}\) from the output from the original two factor ANOVA and recalculate our F-statistics and p-values:
# from the 2-factor ANOVA, MS_wc is the fourth mean squared in the list
MS_wc <- anova3.out$`Mean Sq`[4]
df_wc <- anova3.out$Df[4]
# Atkins
MS_Atkins <- anova3.out.Atkins$`Mean Sq`[1]
df_Atkins <- anova3.out.Atkins$Df[1]
F_Atkins <- MS_Atkins/MS_wc
p_Atkins <- 1-pf(F_Atkins,df_Atkins,df_wc)
# pea soup
MS_peasoup <- anova3.out.peasoup$`Mean Sq`[1]
df_peasoup <- anova3.out.peasoup$Df[1]
F_peasoup <- MS_peasoup/MS_wc
p_peasoup <- 1-pf(F_peasoup,df_peasoup,df_wc)
sprintf('Atkins: F(%d,%d)= %5.4f,p = %5.6f',df_Atkins,df_wc,F_Atkins,p_Atkins)## [1] "Atkins: F(2,114)= 0.2584,p = 0.772759"## [1] "pea soup: F(2,114)= 6.3074,p = 0.002523"The p-values didn’t change much when substituting \(MS_{wc}\), but every little bit of power helps.
19.11 Additivity of Simple Effects
These two simple effects have an interesting relation with the three tests from the original 2-factor ANOVA. It turns out that the SS associated with these two simple effects add up the SS associated with the main effects of Exercise plus the SS for the interaction between Diet and Exercise. In math terms:
\[ SS_{exercise by Atkins diet} + SS_{exercise by pea soup diet} = SS_{exercise} + SS_{exerciseXdiet}\]
You can see that here:
# Adding SS's for the two simple effects of Exercise by Diet:
anova3.out.Atkins$`Sum Sq`[1] + anova3.out.peasoup$`Sum Sq`[1]## [1] 2385.635# Adding SS's for the main effect of Diet and the interaction
# (second and third in the list of SS's)
sum(anova3.out$`Sum Sq`[c(2,3)])## [1] 2385.635Note also that the degrees of freedom for both sets add up to 4
The pie charts below show how \(SS_{total}\) is divided up into the different sums of squares for the standard analysis (main effects and interaction) and for the simple effects analysis.
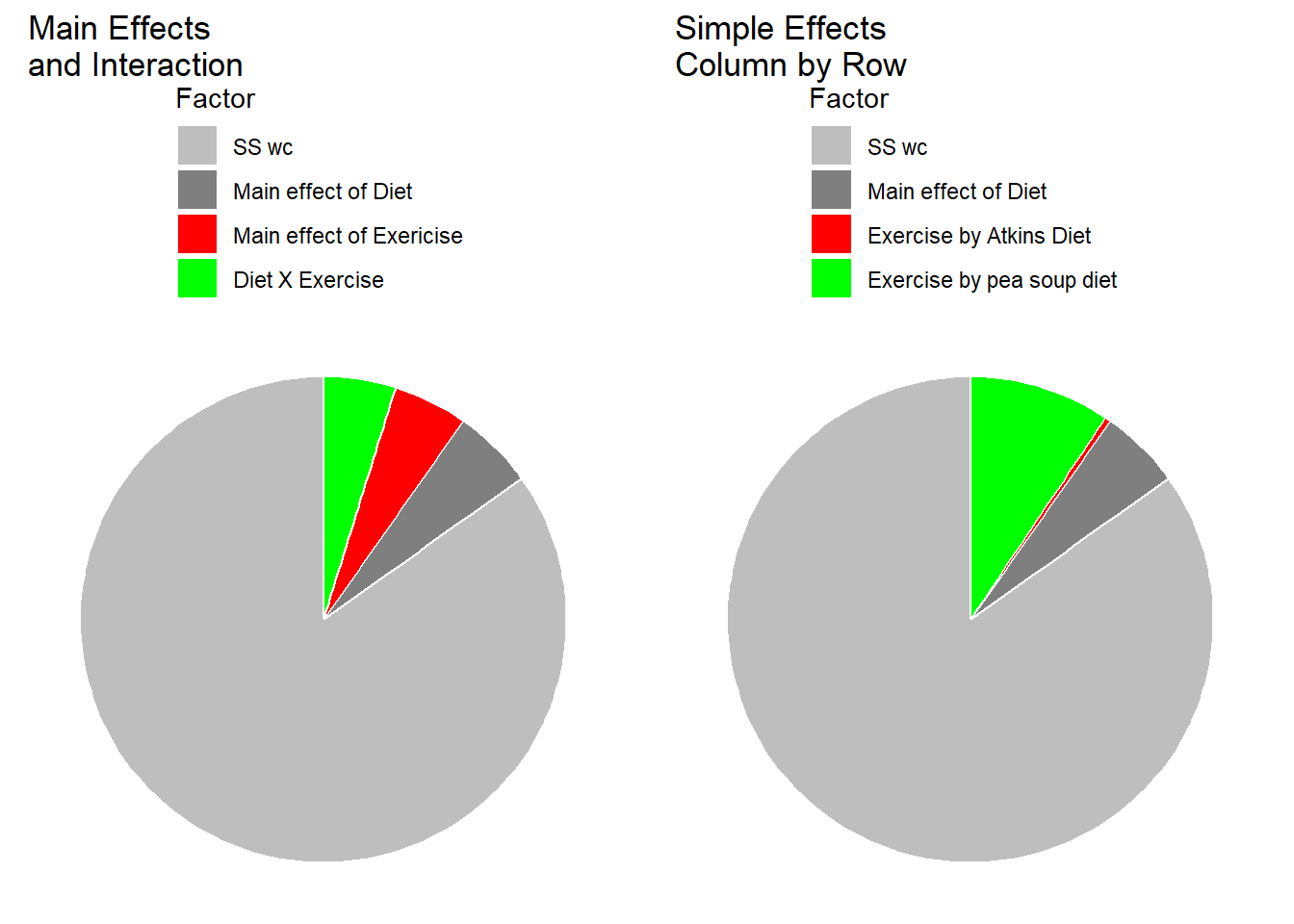
Our simple effects analysis is just another way of breaking down the SS associated with the main effects for columns and the interaction, since the main effect for Diet has no influence on this set of simple effects. You can visualize this by thinking about what would happen to our results of the shapes of the two effects were the same, but if one curve were to be shifted above or below another. For example if our results had come out like this, with an overall higher systolic blood pressure for the Atkins diet:
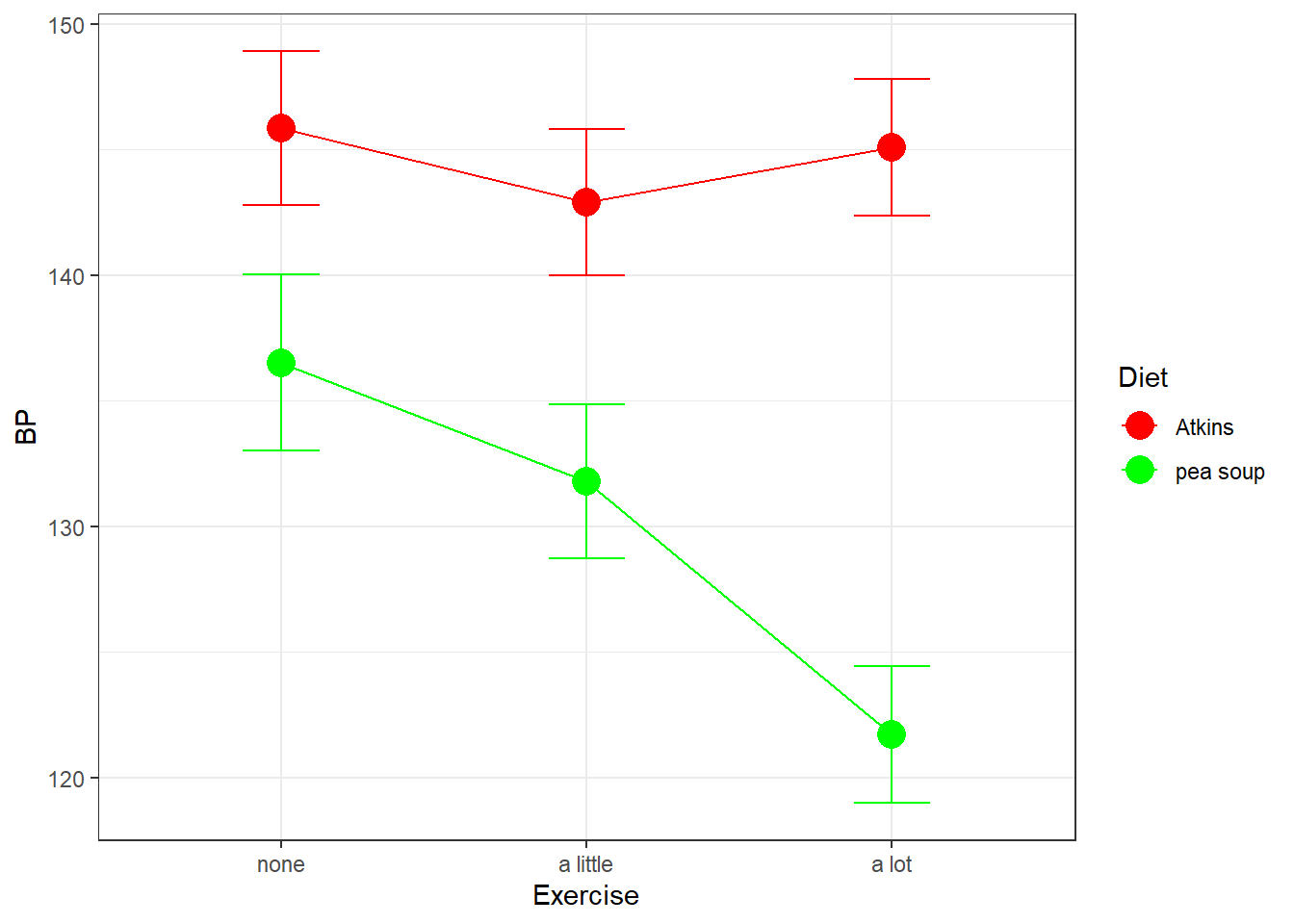
Our simple effects analysis of columns by row would have come out the same. This is because shifting up the Atkins group only increased the main effect of Diet, and not the main effects of Exercise by Diet, the main effect of Exercise, or the interaction between Exercise and Diet.