Chapter 3 Descriptive Statistics

This script will show you how to load in data from the Psych 315 survey and explore some of the data using basic descriptive statistics like measures of central tendency and variability, bar graphs and histograms.

First we’ll clear the workspace and load in the survey data.
R’s function read.csv loads in csv files and if there are headers in the first row uses the names in the headers to name the ‘fields’ that contain the data.

rm(list = ls())
survey <-read.csv("http://www.courses.washington.edu/psy315/datasets/Psych315W21survey.csv")

I’ve told read.csv to put all the data into a variable called ‘survey’.
‘survey’ has a bunch of fields associated with it that correspond to your answers to each of the questions.

For example, I asked students about their heights (in inches). This can be found in the field ‘height’ and can be accessed = with the dollar sign:

survey$height

##   [1] 68 64 63 60 66 70 62 66 61 65 62 72 61 64 67 69 72 71 62 66 62 65 67 60 62
##  [26] 65 62 72 61 65 70 68 67 68 64 66 61 66 67 63 62 64 61 63 68 62 69 72 68 61
##  [51] 67 65 69 62 63 72 68 63 63 68 74 72 61 68 70 70 62 68 61 62 59 63 62 64 71
##  [76] 62 65 62 70 63 67 66 72 66 66 60 65 62 68 75 65 70 65 68 62 62 72 66 74 71
## [101] 68 68 67 64 67 63 65 66 66 65 66 60 67 64 64 62 61 68 66 64 64 67 67 62 65
## [126] 68 63 64 65 74 71 61 68 68 68 63 72 65 64 61 63 66 65 66 69 69 66 63 73 61
## [151] 65 74

To just look at the first few values, use head:

head(survey$height)

## [1] 68 64 63 60 66 70

How many students filled out the survey? This can be determined with the function length for any of the fields:

length(survey$height)

## [1] 152

Mother’s heights are in the field ‘mheight’:

head(survey$mheight)

## [1] 64 62 61 60 61 60

These lists are in the same order across students, so the first student in the list (whoever it is) has a height of:

survey$height[1]

## [1] 68

and has a mother of height

survey$mheight[1]

## [1] 64

Here are some basic statistics about your mother’s heights:

mean:

mean(survey$mheight)

## [1] NA

The answer might be ‘NA’ which means ‘not available’ That’s because there is missing data in the list. Look back and you’ll see that some of the entries are ‘NA’.

To calculate the mean, while ignoring missing entries, use:

mean(survey$mheight,na.rm = TRUE)

## [1] 64

Another way to deal with missing data is to create a new variable without the ’NA’s.

To find the missing data, use ‘is.na’

is.na(survey$mheight)

##   [1] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
##  [13] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [25] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [37] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [49] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [61] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [73] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [85] FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
##  [97] FALSE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE
## [109] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [121] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE
## [133] FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE
## [145] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

gives you ‘TRUE’ for the locations of the missing data.

To find the data that’s NOT missing, use ‘!’ which switches TRUE to FALSE and vice versa:

!is.na(survey$mheight)

##   [1]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE
##  [13]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [25]  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [37]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [49]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [61]  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [73]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [85]  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [97]  TRUE  TRUE FALSE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
## [109]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
## [121]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
## [133]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE
## [145]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE

Finally, we can use this list to pull out the non-missing data, and put it into a new variable ‘mheight’:

mheight <- survey$mheight[!is.na(survey$mheight)]

mean should now work:

mean(mheight)

## [1] 64

The minimum mother’s height with min:

min(mheight)

## [1] 51

and the maximum with max:

max(mheight)

## [1] 72

(sample) standard deviation with sd:

sd(mheight)

## [1] 2.976762

(sample) variance with var:

var(mheight)

## [1] 8.861111

median:

median(mheight)

## [1] 64

or equivalently using quantile:

quantile(mheight,.5)

## 50% 
##  64

Note the ‘50%’ above the result. That’s because quantile returns the result as a ‘named number’. If you want just a regular number without the name, pass the named number through as.numeric:

as.numeric(quantile(mheight,.5))

## [1] 64

The Semi-interquartile range can be calculated using quantile

Q <- as.numeric(quantile(mheight,.75)-quantile(mheight,.25))/2
Q

## [1] 2

We can plot a histogram of mother’s heights like this

# define class intervals based in the min and max:
class.interval <- seq(min(mheight),
                      max(mheight),
                      1)
hist(survey$mheight, 
     main="Histogram of Mother's Heights", 
     xlab="Height (in)", 
     col="blue",
     xaxt='n',
     yaxt = 'n',
     breaks =class.interval
)

# and then adding your own axes with the 'axis' function  
# Axis 1 is 'x' and 2 is 'y':
axis(1, at=class.interval) 
axis(2, at=seq(0,100,5),las = 1) 

What is ratio of men to women in this class? Remember, we can ask which students identified as “Woman” with:

survey$gender == "Woman"

##   [1] FALSE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE
##  [13]  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [25]  TRUE  TRUE  TRUE FALSE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [37]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE FALSE
##  [49]  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE FALSE FALSE  TRUE  TRUE  TRUE
##  [61] FALSE  TRUE FALSE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
##  [73] FALSE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE FALSE  TRUE
##  [85] FALSE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE
##  [97] FALSE  TRUE FALSE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
## [109]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE
## [121]  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE
## [133]  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
## [145]  TRUE  TRUE FALSE  TRUE FALSE  TRUE  TRUE FALSE

The sum function will give you the number of TRUE’s:

number.women <- sum(survey$gender == "Woman")
number.women

## [1] 122

Similarly for the men:

number.men <- sum(survey$gender == "Man")
number.men

## [1] 29

The total number of students is:

total.number <- length(survey$gender)
total.number

## [1] 152

And for women:

100*number.women/total.number

## [1] 80.26316

The percent of men is:

100*number.men/total.number

## [1] 19.07895

Note: these may not add up to 100%. This will happen if some students choose not to answer that question in the survey.

Try this on your own: Calculate the percent of left vs. right handers in the class.

How much do you all play video games? That’s in the field ‘games_hours’

hist(survey$games_hours, 
     main="Histogram of Video Game Playing", 
     xlab="Hours/day", 
     col="blue",
     breaks =seq(0,max(survey$games_hours),.5)
)

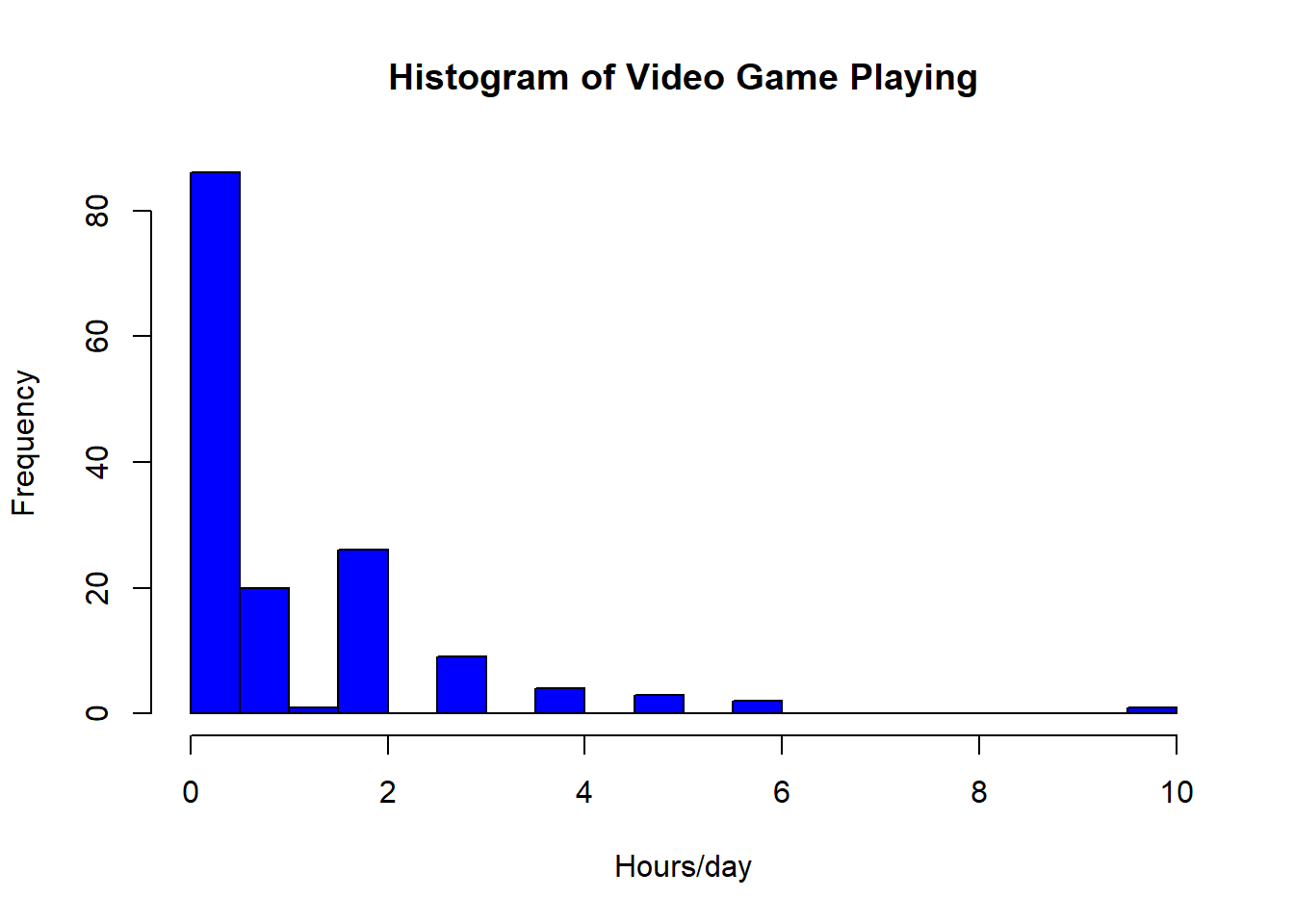Does this distribution look normal? If not is it positively or negatively skewed?

Does video game playing differ by gender?

mean(survey$games_hours[survey$gender == "Man"])

## [1] 1.568966

mean(survey$games_hours[survey$gender == "Woman"])

## [1] 0.8827869

Later on we’ll see if this difference is ‘statistically significant’ using a ‘paired sample t-test’.

What is the distribution of your favorite colors? You’d think we could type hist(survey$color)’ but that doesn’t work because hist needs a list of numbers, not a list of nominal category names.

Fortunately, R has a convenient function table that tabulates nominal scale data into frequencies:

color.freqs <- table(survey$color)
color.freqs

## 
##   Blue  Green Orange   Pink Purple    Red Yellow 
##     44     24      5     25     31     14      9

color.freqs

## 
##   Blue  Green Orange   Pink Purple    Red Yellow 
##     44     24      5     25     31     14      9

This variable color.freqs is something called a ‘table’. It’s like a list of numbers, except that the columns have names associated with them. In our case, the names of the columns are the color names.

Tables are convenient because they let you keep track of what the numbers mean.

You can then send this table into the function `barplot` to make a histogram:

```r
barplot(color.freqs)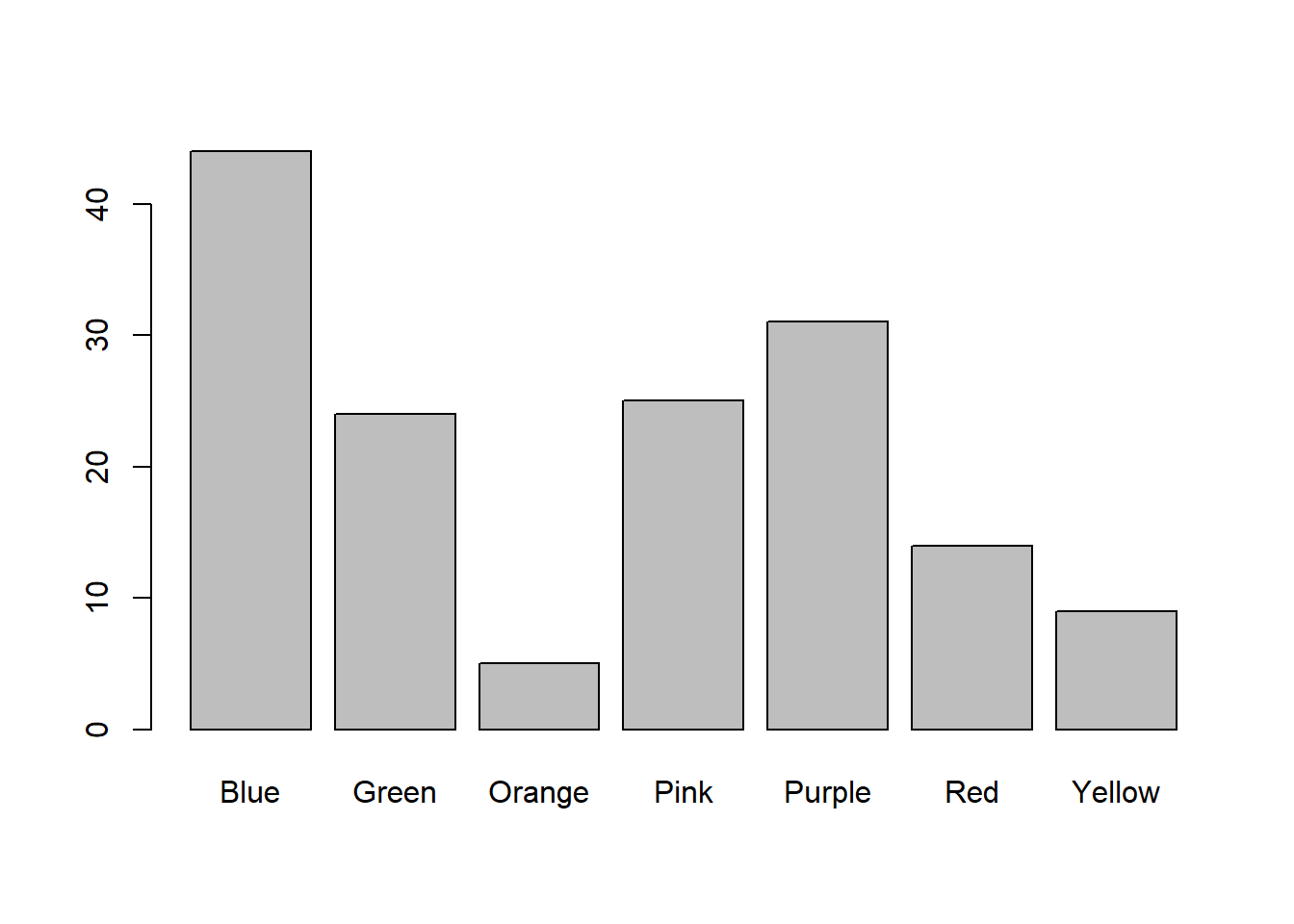

Got to love your love of ‘purple’.

Want to get fancy? Let’s use the option col to color the bars by their color names:

barplot(color.freqs,
        col = c("blue","green","orange","pink","purple","red","yellow") )

Let’s compare the frequency distribution of favorite colors by gender. First we need to create a table frequency distributions for each gender separately, using the ‘table’ function like before. But this time we’ll index into the values for the associated gender:

color.freqs.men <- table(survey$color[survey$gender == "Man"])
color.freqs.women <- table(survey$color[survey$gender == "Woman"])

table will also create 2 (or more) dimensional tables by adding in each factor. Here’s a table of preferred color for all genders:

Next we’ll combine these two tables using the ‘rbind’ function which concatenates rows into a new table:

color.freqs.both <- table(survey$gender,survey$color)
color.freqs.both

##        
##         Blue Green Orange Pink Purple Red Yellow
##            1     0      0    0      0   0      0
##   Man     11     5      0    0      6   6      1
##   Woman   32    19      5   25     25   8      8

You can see that it contains a matrix of numbers along with names for the rows and columns.

This year, there were students that chose not to enter a gender. If we want to exclude this data from the table, we can pull out only the “Man” and “Woman” rows in the table (ignoring the thorny issue of only including students that provided a gender identity):

color.freqs.both <- color.freqs.both[c("Woman","Man"),]

This table is ready to be plotted using barplot. We’ll use the option beside = TRUE so the “Men” and “Women” bars are plotted next to each other instead of on top of each other.

barplot(color.freqs.both,
        beside = TRUE,
        legend = c("Men","Women"),
        col = c("Blue","Red"))

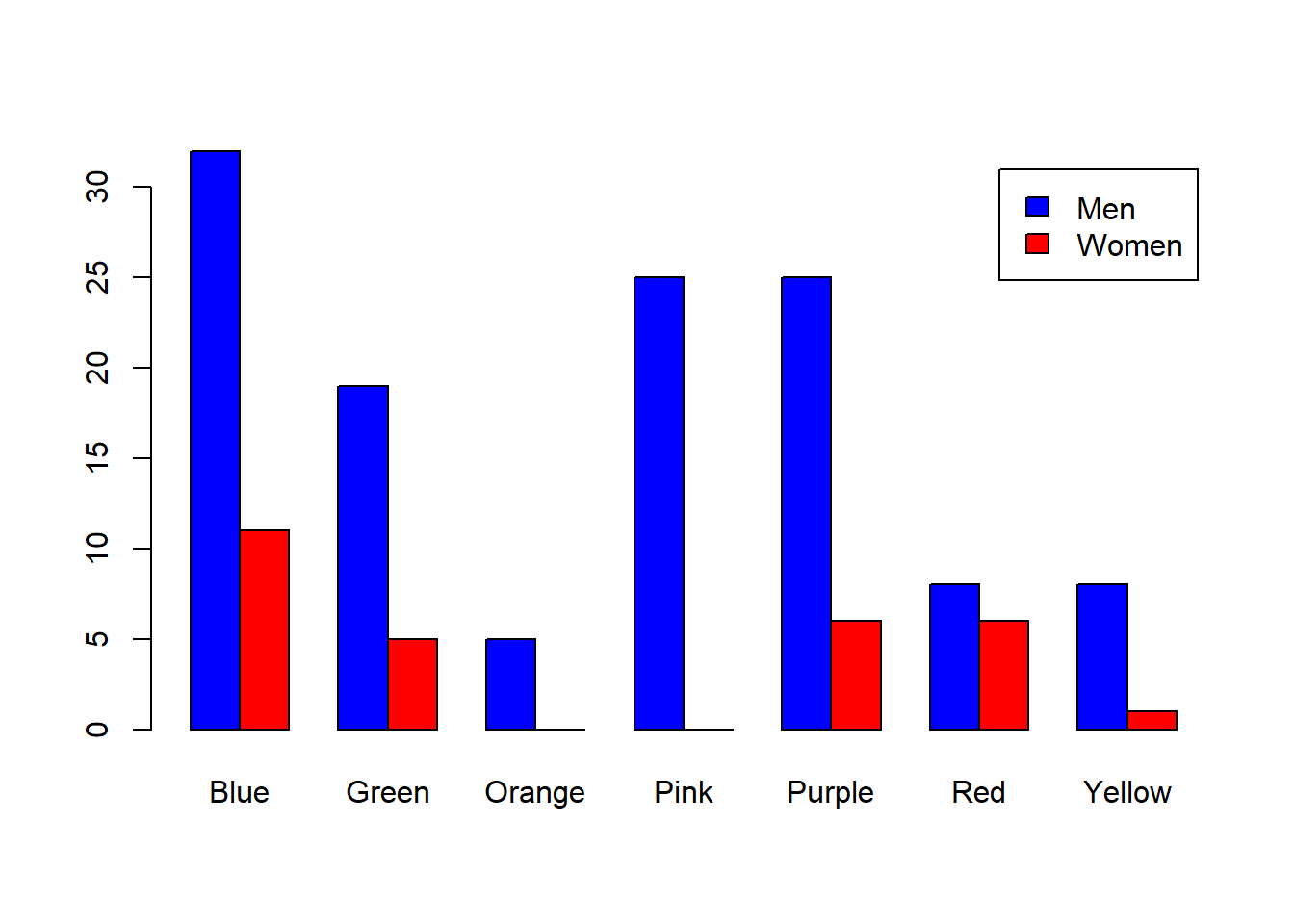Do you think there is a difference in the distribution of color preference across gender? Later on we’ll determine if these two distributions are significantly different from each other using a ’Chi-squared test for independence`.

As an exercise, see if you can create a histogram of the number of birthdays for each month The months you all were born in is in survey$month:

As before, we can make a table and plot it as a bar plot:

month.table <- table(survey$month)
barplot(month.table)

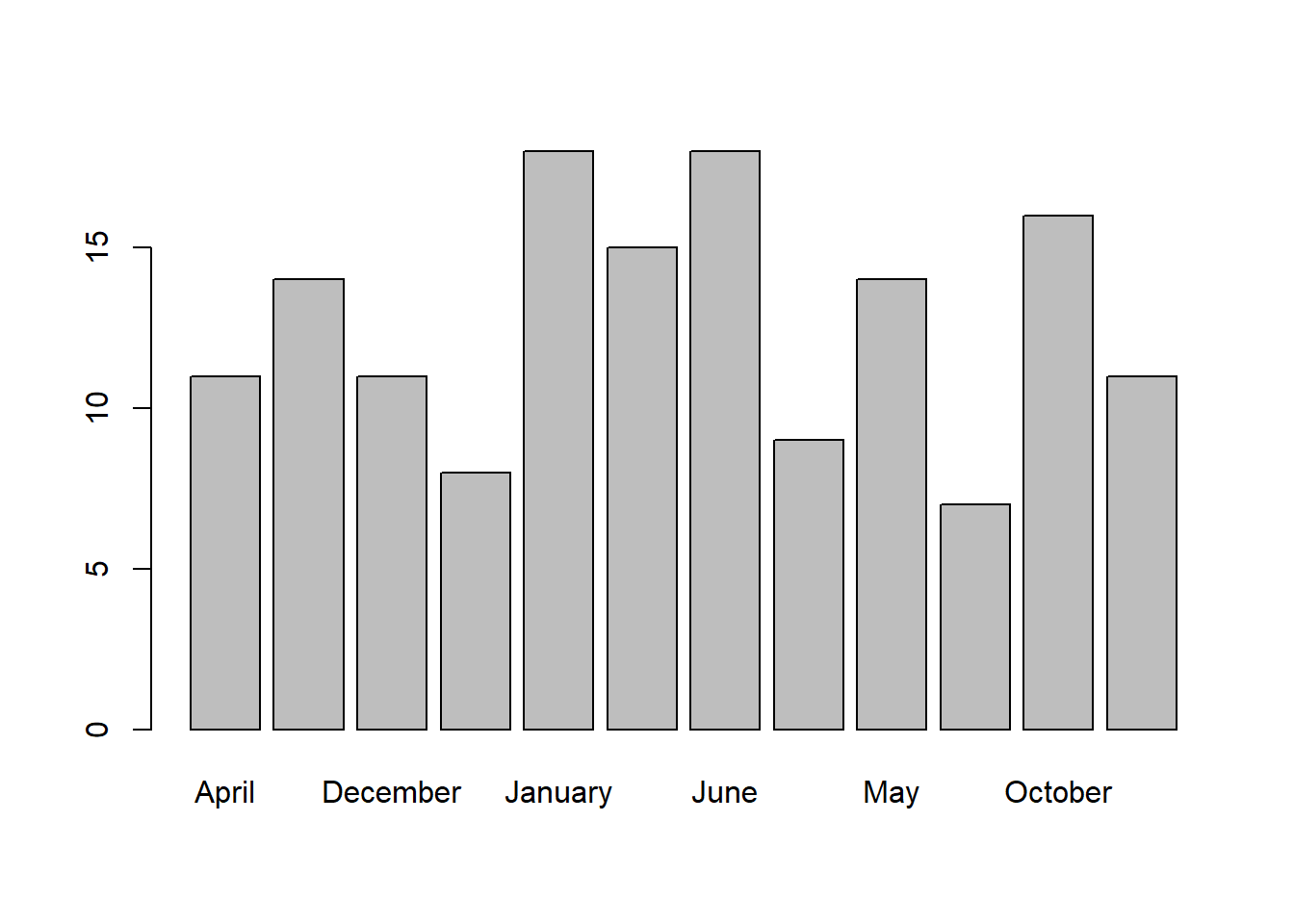By default, table organizes the categories in alphabetical order. That’s not what we want. Look at the table:

month.table

## 
##     April    August  December  February   January      July      June     March 
##        11        14        11         8        18        15        18         9 
##       May  November   October September 
##        14         7        16        11

You can see it’s in alphabetical. To reorder the table, we can re-index the values by noting January, came 5th, Feburary came 4th, and so on.

To rearrange the order we can do this:

month.table <- month.table[c(5,4,8,1,9,7,6,2,12,11,10,3)]

Where the list 5,4,8,… are the locations for January, February, March, etc.

Now look:

month.table

## 
##   January  February     March     April       May      June      July    August 
##        18         8         9        11        14        18        15        14 
## September   October  November  December 
##        11        16         7        11

It’s in the proper order. Now the bar plot will look right:

barplot(month.table)

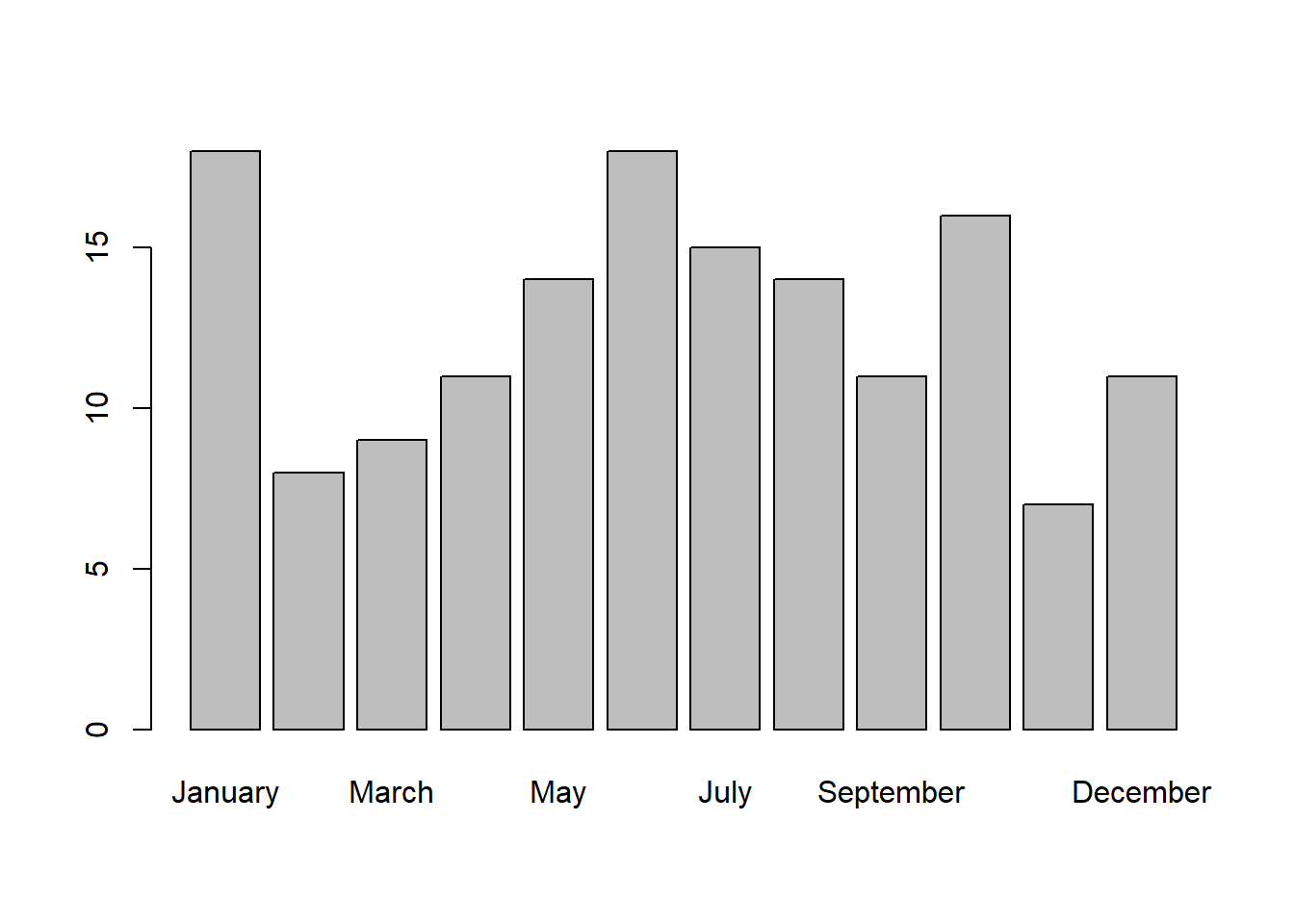There are more students born in some months than others. Do you think this happened just by chance? Or is this distribution particularly unsual? Later on we’ll run a ‘Chi-Squared’ test to determine how likely we’d get a data set like this by chance.

Finally, let’s find the average amount of sleep for the women that like to sit near the front of the class:

To find these students we need to find those for which BOTH their gender is Woman AND their favorite color is ‘Purple’. This requires us to use & (and) to compare lists of TRUE and FALSE

& compares two TRUE/FALSE variables and returns ‘TRUE’ if both are TRUE

TRUE & TRUE

## [1] TRUE

TRUE & FALSE

## [1] FALSE

FALSE & TRUE

## [1] FALSE

FALSE & FALSE

## [1] FALSE

Here’s how to use & to find the women that like to sit near the front of the class:

students.gender.front <- survey$gender== 'Woman' & survey$sit == 'Near the front'

And here’s the average amount of sleep they get each night:

mean(survey$sleep[students.gender.front],na.rm = TRUE)

## [1] 7.204545

We use | for ‘or’. This returns TRUE if either are TRUE:

TRUE | TRUE

## [1] TRUE

TRUE | FALSE

## [1] TRUE

FALSE | TRUE

## [1] TRUE

FALSE | FALSE

## [1] FALSE

Let’s use | to find the favorite color for students that were either born in January or are left-handed:

students.january.left = survey$month == "January" | survey$hand == "Left"
survey$color[students.january.left]

##  [1] "Blue"   "Blue"   "Purple" "Blue"   "Green"  "Purple" "Green"  "Red"   
##  [9] "Red"    "Purple" "Pink"   "Blue"   "Red"    "Red"    "Green"  "Purple"
## [17] "Pink"   "Green"  "Orange" "Purple" "Green"  "Blue"   "Pink"   "Blue"