Chapter 11 Two Sample Dependent Measures t-test
This test is used to compare two means for two samples for which we have reason to believe are dependent or correlated. The most common example is a repeated-measure design where each subject is sampled twice- that’s why this test is sometimes called a ‘repeated measures t-test’.
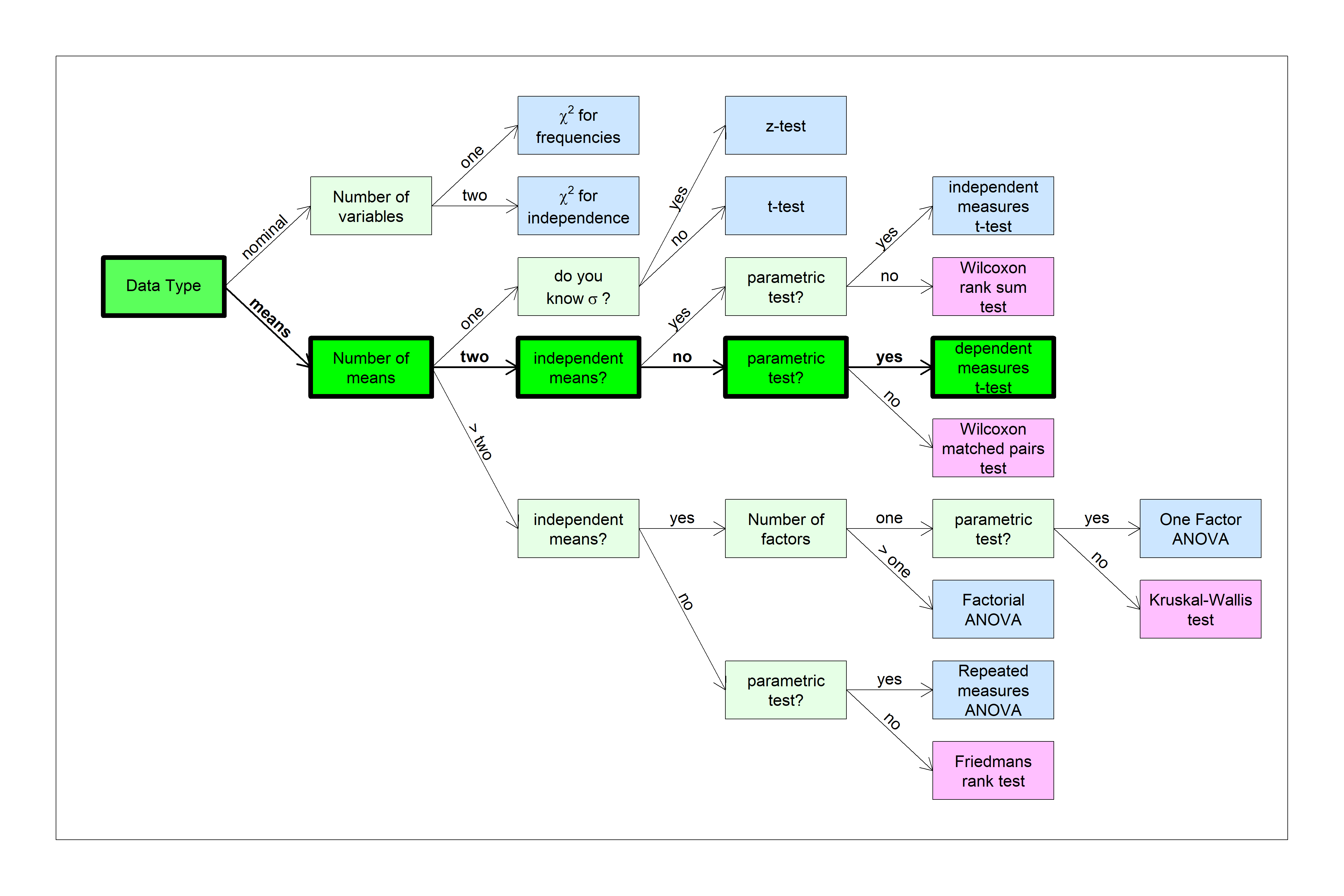
You can find this test in the flow chart here:
Consider a weight-loss program where everyone lost exactly 10 pounds. Here’s an example of weights before and after the program (in pounds) for 10 subjects:
| Before | After |
|---|---|
| 137 | 127 |
| 154 | 144 |
| 133 | 123 |
| 182 | 172 |
| 157 | 147 |
| 134 | 124 |
| 160 | 150 |
| 165 | 155 |
| 162 | 152 |
| 144 | 134 |
The mean weight before the program is 152.8 pounds and the mean after is 142.8 pounds. This should be considered a hugely successful program. But if you run an independent measures t-test on these two samples, you’d get a t-score of t(18) = 1.42, and p-value of p = 0.1725. You’d have to conclude that the program did not produce a significant change in weight.
But everyone lost 10 pounds! How could we not conclude that the weight loss program was effective? The problem is that there is a lot of variability in the weights across subjects. This variability ends up in the pooled standard deviation for the t-test.
But we don’t care about the overall variability of the weights across subjects. We only care about the change due to the weight-loss program.
Experimental designs like this where we expect a correlation between measures are called ‘dependent measures’ designs. Most often they involve repeated measurements of the same subjects across conditions, so these designs are often called ‘repeated measures’ designs.
If you know how to run a t-test for one mean, then you know how to run a t-test for two dependent means. It’s that easy.
The trick is to create a third variable, D, which is the pair-wise differences between corresponding scores in the two groups. You then simply run a t-test on the mean of these differences - usually to test if the mean of the differences, D, is different from zero.
11.1 High School vs. College GPAs
Let’s go to the survey and see if there is a significant difference between the men students’ high school and college GPAs. This is a repeated measures design because each student reported two numbers. We’ll run a two-tailed test with \(\alpha\) = 0.05.
There are 28 students that identify as men in the class. The first step is to calculate the difference between the GPA’s from high school and Uw for each student. Here’s a table with a third column showing the differences which we’ll call D:
| HS | UW | D |
|---|---|---|
| 3.40 | 3.23 | 0.17 |
| 4.00 | 3.65 | 0.35 |
| 3.95 | 3.80 | 0.15 |
| 3.85 | 3.66 | 0.19 |
| 3.65 | 3.30 | 0.35 |
| 3.87 | 3.68 | 0.19 |
| 2.90 | 3.83 | -0.93 |
| 3.20 | 3.90 | -0.70 |
| 3.70 | 3.43 | 0.27 |
| 4.60 | 2.60 | 2.00 |
| 3.70 | 3.80 | -0.10 |
| 3.80 | 3.85 | -0.05 |
| 3.00 | 3.00 | 0.00 |
| 3.83 | 3.35 | 0.48 |
| 3.80 | 3.31 | 0.49 |
| 3.60 | 2.00 | 1.60 |
| 3.89 | 3.84 | 0.05 |
| 4.00 | 3.91 | 0.09 |
| 2.18 | 2.89 | -0.71 |
| 3.70 | 3.07 | 0.63 |
| 2.20 | 4.00 | -1.80 |
| 3.95 | 3.66 | 0.29 |
| 3.88 | 3.53 | 0.35 |
| 3.50 | 3.51 | -0.01 |
| 3.70 | 3.20 | 0.50 |
| 3.20 | 3.30 | -0.10 |
| 3.20 | 3.65 | -0.45 |
| 3.92 | 3.95 | -0.03 |
An dependent measures t-test is done by simply running a t-test on that third column of differences. The mean of differences is \(\overline{D}\) = 0.12. The standard deviation of the differences is \(S_{D}\) = 0.7013.
You can verify that this mean of differences is the same as the difference of the means: the mean of the high school GPAs is 3.58 and the mean of the UW GPAs is 3.46. The difference between these two means is 3.46 - 3.46 = 0.12, which is the same as \(\overline{D}\).
The standard error of the mean for D is:
\[s_{\overline{D}} = \frac{s_{D}}{\sqrt{n}} = \frac{0.7013}{\sqrt{28}} = 0.1325\]
Just like for a t-test for a single mean, we calculate our t-statistic by subtracting the mean for the null hypothesis and divide by the estimated standard error of the mean.
\[t = \frac{\overline{D}}{s_{\overline{D}}} = \frac{0.1168}{0.1325} = 0.8812\]
And since we’re dealing with 28 pairs, our degrees of freedom is \(df = n-1 = 27\)
Since this is a two-tailed test, we can use pt to find the p-value like this:
## [1] 0.3859869Our p-value is greater is than \(\alpha\) = 0.05. We therefore fail to reject \(H_{0}\) and conclude that the high school GPA’s are not statistically different from the college GPAs.
11.2 Effect size (d)
The effect size for the dependent measures t-test is just like that for the t-test for a single mean, except that it’s done on the differences, D. Cohen’s d is :
\[d = \frac{|\overline{D} - \mu_{hyp}|}{s_{D}}\]
For this example on GPA’s
\[d = \frac{|\overline{D}|}{s_{D}} = \frac{|0.1168|}{0.7013} = 0.1665\]
This is considered to be a small effect size.
11.3 Power for the two-sample dependent measures t-test
Calculating power for the t-test with dependent means is just like calculating power for the single-sample t-test. For the power
calculator, we just plug in our effect size, our sample size (size of each sample, or number of pairs), and alpha. For our example of an
effect size of 0.1665273, sample size of 28, 28 and \(\alpha = 0.05\), we can use power.t.test. For the dependent measures test we set type = "paired".
power.out <- power.t.test(n=28,delta=0.1665,sig.level=0.05,type ="paired",alternative = "two.sided")## [1] 0.1335137Actually, since this is the same as a one-sample t-test, we get the same answer if we use type = "one.sample":
power.out <- power.t.test(n=28,delta=0.1665,sig.level=0.05,type ="one.sample",alternative = "two.sided")## [1] 0.1335137To find out how many student’s we’d need to get a power of 0.8 we use n = NULL and power = 0.8:
power.out <- power.t.test(n=NULL,delta=0.1665,power = 0.8,sig.level=0.05,type ="paired",alternative = "two.sided")The answer is in power.out$n:
## [1] 285.052311.4 Example 2: Heights of Men in the Class vs. Their Father’s Heights
Let’s see if there’s a statistically significant difference between the heights of the men students and their fathers. This time we’ll go straight to the survey data and run the test using t.test rather than doing it by hand like the last example. This procedure is almost identical to what we used in for the t-test for independent means.
survey <- read.csv("http://www.courses.washington.edu/psy315/datasets/Psych315W21survey.csv")
x <- survey$height[survey$gender == "Man"]
y <- survey$pheight[survey$gender == "Man"]We’re ready for t.test. If you send in both x and y, t.test. To run a dependent measures t-test we use paired = TRUE.
Here’s where you can find the information needed to report your results in APA format:
## [1] "t(25) = 1.60, p = 0.1219"Our p-value is greater is than \(\alpha\) = 0.05. We therefore fail to reject \(H_{0}\) and conclude that the heights of the men students are not statistically different from their father’s heights.
Now that you know that a dependent measures t-test is the same as a one-sample t-test on the differences, see why we get the same result this way:
out <- t.test(x-y,alternative = "two.sided",alpha = .05)
sprintf('t(%g) = %4.2f, p = %5.4f',out$parameter,out$statistic,out$p.value)## [1] "t(25) = 1.60, p = 0.1219"One thing to note: There may be NA’s in the data, but by default, t.test removes values that have a NA in rows of either x or y. If you want to be explicit, you can send in na.action = "omit", which is the default.